ZEMAX OpticStudio 如何对中频误差进行评估和公差分析
本内容更加贴近光学元件的制造和加工,如果您对这方面感兴趣,本文将会很有帮助!
如何对中频误差进行评估和公差分析


概述

本文我们介绍了如何使用周期性空间频率表面来建模旋转对称曲面的不规则度(例如由于金刚石车削而产生的不规则度)。
具体方法为使用专用的自定义序列模式表面DLL(常规偶次非球面结合Zernike项与矢高周期变化得到)建模该中空间频率表面。我们将使用中频面周期性不规则度对非球面单透镜和一个天塞物镜 (Tessar Objective) 进行表面不规则度的评估和公差分析。
见附件

介绍

对于表面不规则度的公差分析是镜头设计过程中保证生产加工得到的实际光学元件能够达到预期性能的重要环节。可能引起光学性能变化的因素包括但不限于光学表面的加工误差、所用模具的加工误差、注塑造成的不规则度、光学元件与传感器间的校准误差、光学表面的粗糙度误差以及厚度误差。
将这些不规则度参数化将有利于公差分析,公差操作数 TEZI 就是一个很好的例子。TEZI 操作数使用 Zernike 多项式来表示不规则度,一些低频表面误差可以用该参数化公式来评价公差。并且非常高频的表面误差将引起光束产生大角度散射,光学系统中可以将这部分作为能量损耗忽略不计。然而,介于这两者之间的中频表面误差,参数化建模就存在一些难度,不仅在于难以使用多项式进行表示,而且在于不能作为系统损耗而忽略。
本文我们以以金刚石车削为例,解释为什么需要一个中频误差的分析模型。我们定义了一个表达式来建模这种不规则度,并在示例中使用点列图和公差分析进行展示。最后,说明使用这种模型时应注意的限制条件。
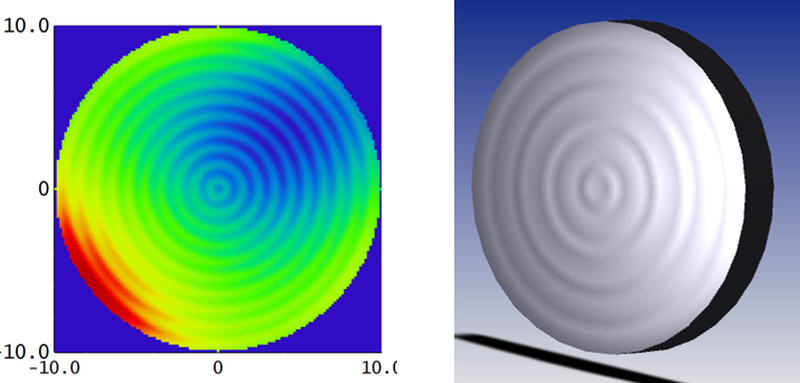

光学制造

在光学表面制造时,通常用表面不规则度或RMS误差的形式来衡量一个表面与一个完美标准表面之间的差异。例如,在632.8 nm的He-Ne激光测试下,一个成品透镜或反射镜的表面不规则度大概为0.1λRMS。再以定制透镜为例,如零位检验中使用的透镜,表面不规则度大概为0.01 λRMS。

空间频率分为不同的频域:
如果空间频率高,类似于表面粗糙度,我们可以将其考虑为光学系统的损耗
如果空间频率低,对于低频部分我们可以用如 Zernike 多项式等方法表示其形状变化
当空间频率高至无法使用多项式轻松定义(孔径中包含10个周期以上[2])或空间频率低至其造成的影响不能忽略时(相对于波长的波纹周期大于从给定的表面到像面光路的1/10[2,3]),我们统称为中频部分。
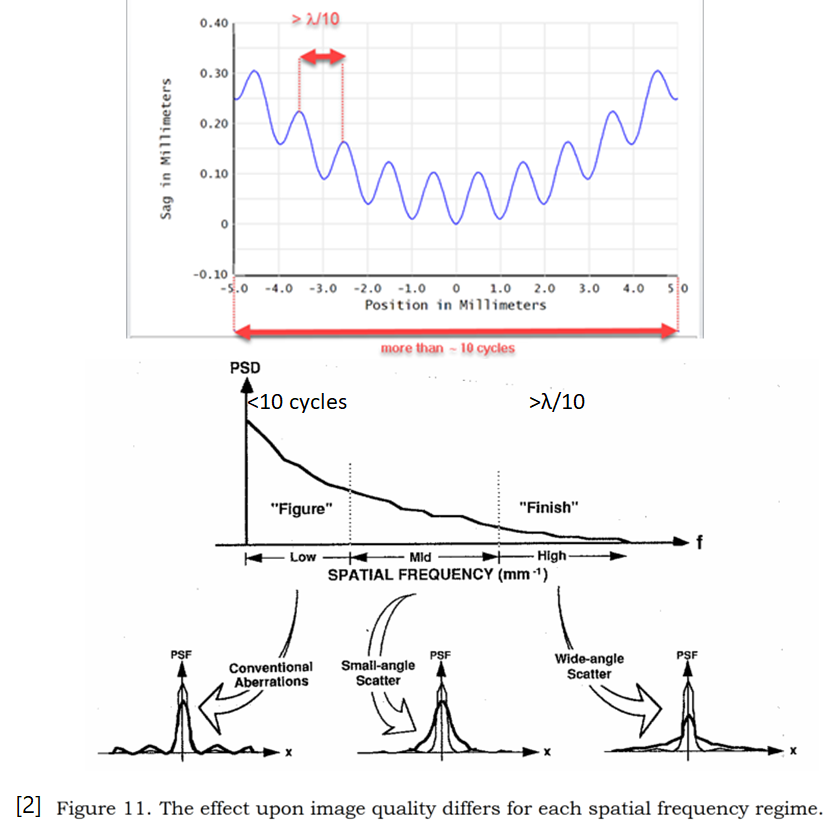
这些中频误差可能导致系统分辨率降低、产生杂散光、降低照明系统均匀性等。因此在绘制图纸或订购零件之前,这些误差应体现在光学元件公差分析中。如果是专门定制的零件,与制造商结合空间频率详细讨论表面不规则度形式是至关重要的,制造商可能会提供类似零件的性能数据或者提供一个最接近的不规则度结果预测。
通常情况下,不规则度的形式是未知的。如果是常规抛光,那么假定不规则度会引起低阶像差(如光焦度和像散)比较保险,并可以在OpticStudio中使用多种不同方法模拟这种不规则度。然而,与传统的表面加工不同,金刚石车削可以作为一个特别的案列,需要预测零件中的中频至高频旋转对称波纹。
金刚石车削是以金刚石为切削工具的车削方法,广泛应用于从晶体、金属、丙烯酸等材料的高质量非球面光学元件加工中,塑料光学元件也通常使用金刚石车削加工得到的模具来注塑成型。它是一种用镶金刚石刀头的旋转车刀对精密元件进行机械加工的过程,根据加工工艺的不同可以产生从P-V深度为0.1微米的中高频误差或几个微米的低频误差。常见相关术语为“单点金刚石车削 (SPDT) ”。金刚石车削可以获得高的反射亮度,因此不需要额外的抛光或抛光。然而,金刚石刀头的轨迹会在零件局部留下一定频率的波纹。

中空间频率表面可能的表达式

在OpticStudio或光学系统中,有多种方法可能用于表达不规则度:
Zernike 项模拟表面不规则度
网格数据表示表面不规则度
利用扩展多项式或切比雪夫多项式得到的三维误差对加工表面的轮廓数据进行拟合
扩展奇次非球面可以拟合旋转对称测量数据
多项式的参数拟合在高频上往往表现不佳,因为表面上波纹的数量取决于参数方程中多项式的数量。随着高频误差的增加,仅依靠多项式拟合可能会变得不准确。此外,当使用过多多项式或者网格矢高点时,将不存在一个像蒙特卡罗那样的实用公差统计分析方法来分析它们可能包含的各种不规则度。
我们可以从加工过程中预测金刚石车削引起的中频旋转对称不规则度[3]。本文我们提出一种将多个表面组合起来,以形成一个用户自定义表面的方法,来完成诸如公差分析这类需要改变参数的任务。
表达式如下所示:
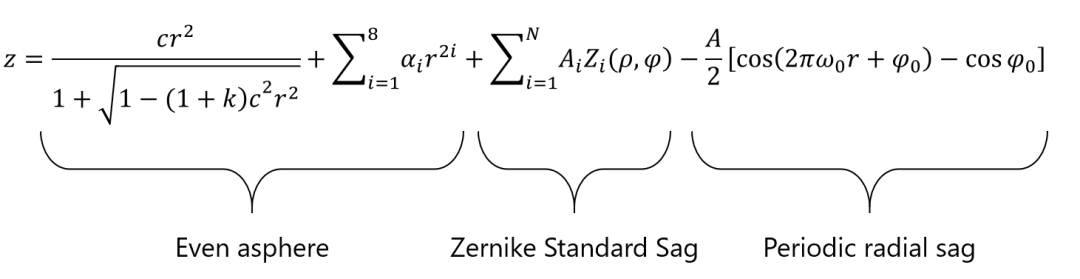
上述表达式包含三个部分,从左至右分别是:偶次非球面部分,Zernike部分,周期矢高部分。其中,Zernike部分与 Zernike Standard矢高面型完全相同,使用的是 Zernike 多项式。Zernike 多项式为单位圆环上一系列正交的多项式。周期性部分是以一个固定振幅和频率叠加到表面上的矢高值,其形式与 OpticStudio 内置的 “us_eaperiodic.dll” 相同。中频表达式可以看做是 Zernike Standard 矢高叠加上一个周期性变化的一种变体,其中:
z 是表面矢高
r 是以透镜单位为单位的极坐标矢径长度
c 是曲率
k 是圆锥系数
αi 第i个非球面的系数
N 是 Zernike 系数的个数
Ai 第 i 个 Zernike Standard 多项式的系数
ρ 是光线归一化径向坐标
φ 是光线角向坐标
A 是周期项振幅
ω0 是周期项频率(单位是长度单位的倒数)
φ0 是相位偏移,如镜头数据编辑器中采用角度制输入,但是计算时转换为弧度制

中空间频率表面的实现方法

为了描述中频表面的建模应用,我们将使用附件中的"SpatialFrequency_implementation.zar"文件作为示例,或者也可以提取其中的“us zernike+msf.dll“文件,并将其保存在{Zemax}\documents\Zemax\DLL\Surfaces中的文档文件夹中。
让我们来查看中频表面的设置:首先,像其他所有面型一样,我们需要打开表面属性,将表面类型改为用户自定义,并选择 “us\u zernike+msf.dll"。

DLL加载到表面上后,我们就可以看到我们所需的参数。如下图所示,非球面项以16阶结束,然后是周期性径向矢高的三个参数 A、w0、phi0。Zernike参数叠加周期性矢高,就完成了用户定义表面的定义。

由于我们的用户定义曲面“us_zernike+msf.dll”是从Zernike Standard 矢高面型和另一个用户定义曲面“us_eaperiodic.dll”派生的,因此我们可以先研究一下它们,再比较一下我们的新面型有什么不同。
首先,让我们比较一下"us_eaperiodic.dll"和我们的中频面 "us_zernike+msf.dll",让二者使用相同的设置,具体采用:
振幅 A = 0.01mm
频率 w0 =1 cycle/mm
相位 φ0 = 0.01 degrees

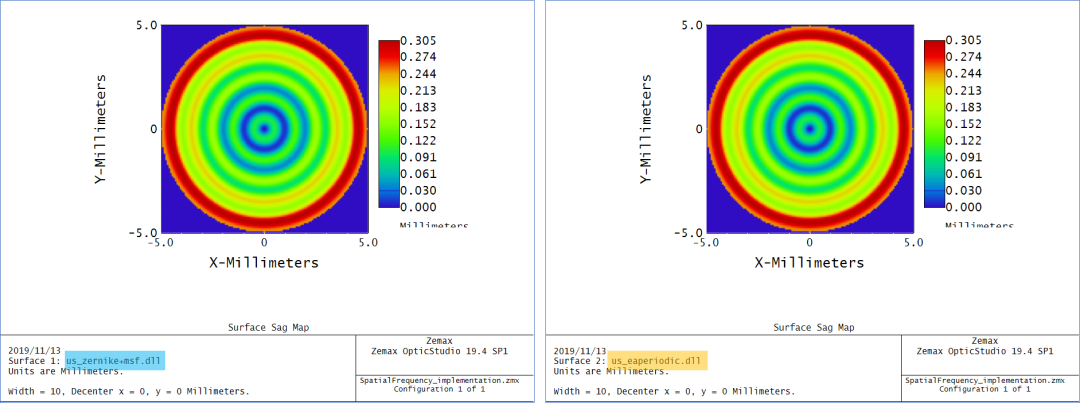
我们看到,左侧的中频曲面“us_zernike+msf.dll”(以蓝色突出显示),右侧的周期曲面“us_eaperiodic.dll”(以橙色突出显示)具有相同的曲面矢高轮廓。
同样,让我们对比一下 Zernike Standard 矢高曲面和我们的中频面“us_Zernike+msf.dll”有何异同。我们将使两个曲面在其设置中完全相同,并检查与 Zernike 项的一致性。具体设置为:
Zernike X 偏心 = 0.2
Zernike Y 偏心 = -0.1
Zernike 1 = 1.00E-003
Zernike 2 = -4.00E-003
Zernike 3 = -2.00E-003
Zernike 4 = 1.00E-003
Zernike 5 = 5.00E-004
Zernike 6 = 1.00E-004
Zernike 7 = 2.00E-003
Zernike 8 = 1.00E-003
Zernike 9 = -5.00E-003
Zernike 10 = 1.00E-003


我们看到,左侧的中频曲面“us_zernike+msf.dll”(以蓝色突出显示)和右侧的 Zernike Standard 矢高曲面(以橙色突出显示)具有相同的曲面矢高轮廓。
所以,我们可以放心大胆地假设:中频曲面同时具有周期曲面和Zernike多项式的性质,当然还有标准的非球面轮廓。下面显示了具有Zernike多项式不规则度和周期性波纹状不规则度的曲面的示例,以供说明。
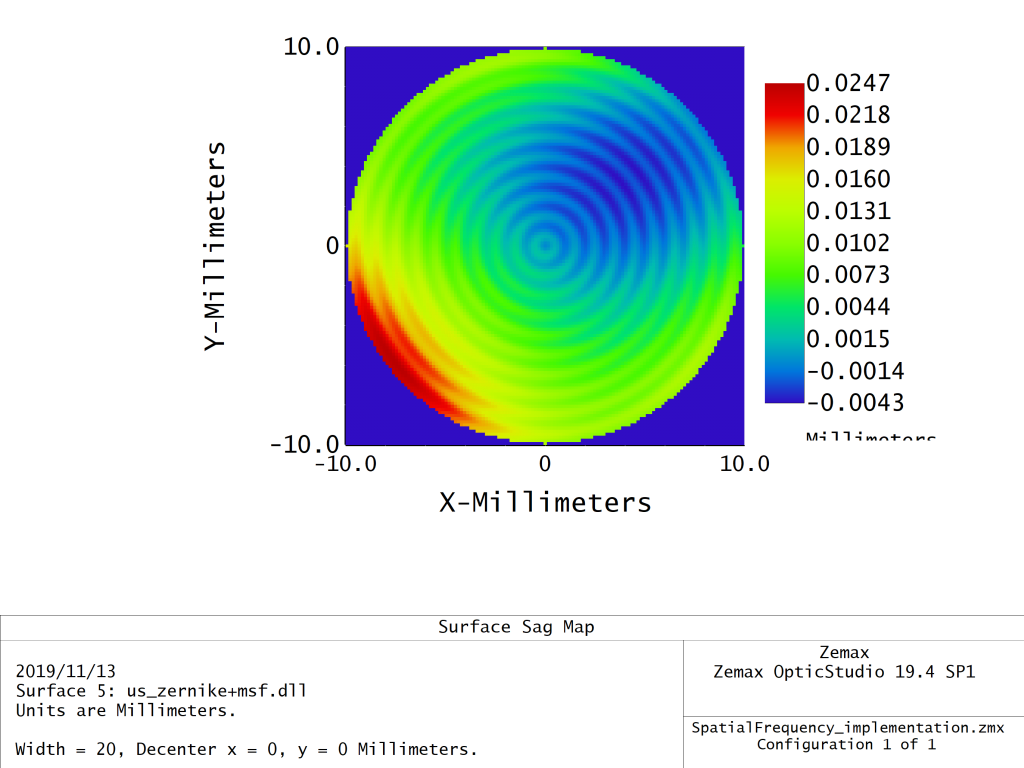
本文使用的DLL已在附件中提供。
简单周期面“us_eaperiodic.dll”及其源代码可以在根目录\Documents\Zemax\DLL\Surfaces中找到,这是OpticsStudio安装时就自带的表面。

应用示例 1: 非球面单透镜点列图

此示例用于观察中频曲面的点列图,我们将使用本文附件中的“spatial frequency_spot diagrams.zar”文件。
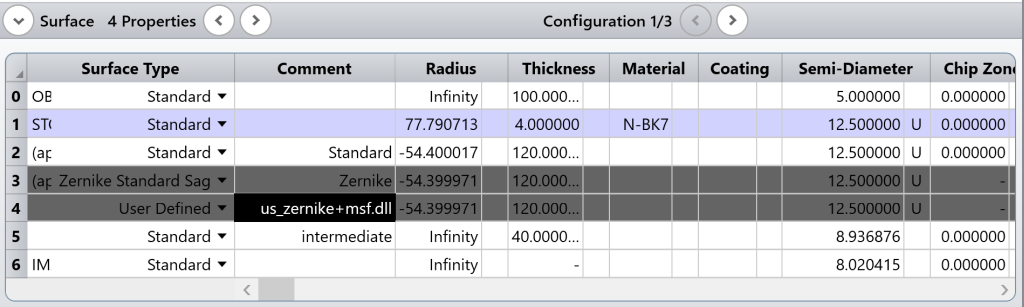
设计目标为物高 5mm,物距 100mm,后焦 160mm的非球面透镜,分别采用三个表面:
一个标准面
一个 Zernike Standard 矢高面
使用 "us_zernike+msf.dll" 建立的中频面。
其中Zernike Standard 矢高面和中频面参数相同,具体为:
振幅 = 5.00E-004mm
频率 w0 =1 cycle/mm
相位 φ0 = 0.00 degrees
Zernike X 偏心 = 0.2
Zernike Y 偏心= -0.1
Zernike 1 = 1.00E-003
Zernike 2 = -4.00E-003
Zernike 3 = -2.00E-003
Zernike 4 = 1.00E-003
Zernike 5 = 5.00E-004
Zernike 6 = 1.00E-004
Zernike 7 = 2.00E-003
Zernike 8 = 1.00E-003
Zernike 9 = -5.00E-003
Zernike 10 = 1.00E-003
从光线出射端测试,为了方便观测,中频面放在距离像面40 mm的位置:

我们可以看到非常经典的旋转对称的标准面光斑轮廓。Zernike Standard 矢高面由于Zernike多项式项的存在,显示出轻微变形的光斑轮廓。中频曲面具有相同的Zernike多项式参数,此外还有周期参数,表现为光斑中的圆环。
在像面,我们用下面的结构矩阵点列图 (Configuration Matrix Spot Diagram) 来说明这一点。结构1为标准面,结构2为 Zernike Standard 矢高面,结构3为中频曲面。
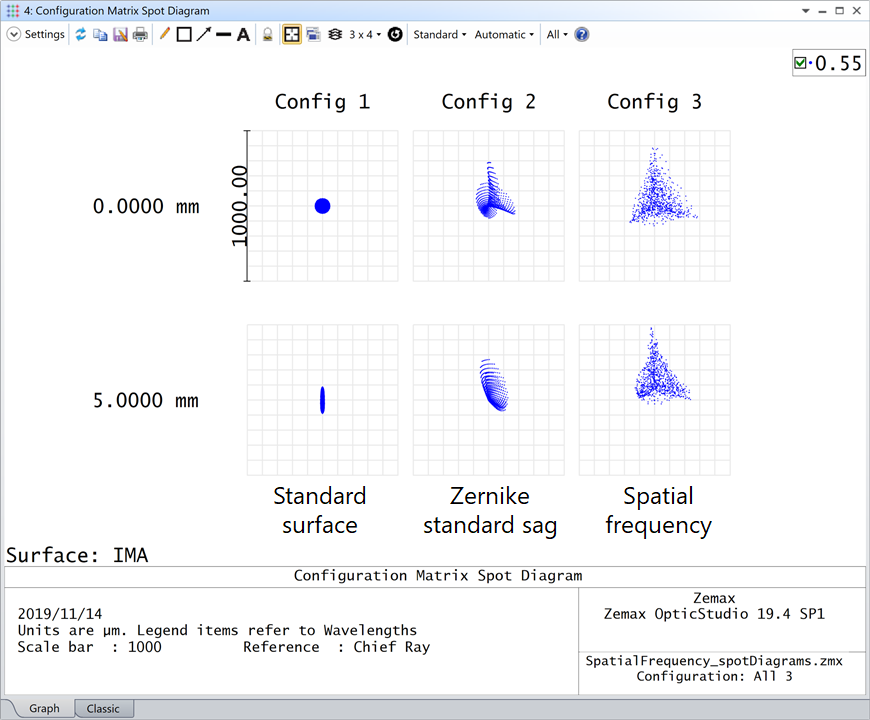
标准表面没有不规则度,它也将作为我们的参考标准。Zernike Standard 矢高面稍微有些变形。中频曲面大体上与 Zernike Standard 矢高面相同,但由于曲面上形成的波纹形状,产生了相对于 Zernike 光斑轮廓不同的周围散射光线。我们可以预期这样的镜头制造时会有部分镜头会因光线改变了预定路径而不符合设计的表面规定。

应用示例 2: 天塞物镜公差分析

此示例用于观察天塞物镜中频表面的公差,我们将使用文章附件中“spacealfrequency_tol.zar”文件。
我们使用的是Paul Rudolph (USP721240)[4] 的经典天塞镜头设计,系统的第一个表面上为中空间频率表面(橙色突出显示)。


以下图所示的参数设置公差向导用于公差分析:
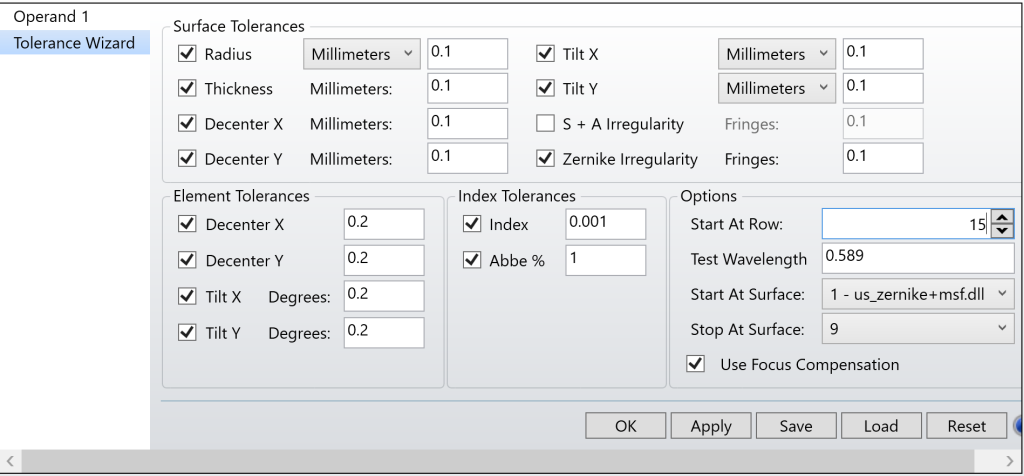
在OpticStudio中,TEZI公差操作数允许对具有轴上孔径的标准面、非球面或环形面表面的不规则性进行自动公差扰动,其他表面类型则不允许使用 TEZI。但我们可以仍使用 TPAR 来扰动曲面的参数,多边形物体和CAD文件(如STEP和IGES文件)则无法进行扰动。
设置参数为:
振幅= 5.00E-004mm
频率 w0 =1 cycle/mm
相位 φ0 = 0.00 degrees
Zernike X 偏心 = 0.2
Zernike Y 偏心 = -0.1
Zernike 1 = 1.00E-003
Zernike 2 = -4.00E-003
Zernike 3 = -2.00E-003
Zernike 4 = 1.00E-003
Zernike 5 = 5.00E-004
Zernike 6 = 1.00E-004
Zernike 7 = 2.00E-003
Zernike 8 = 1.00E-003
Zernike 9 = -5.00E-003
Zernike 10 = 1.00E-003
这些参数表示 Zernike 项在整个表面上具有约 5 微米的 RMS 误差,周期项振幅约为 0.5 微米,周期为 1 周期/毫米,或者说在整个表面有 20 个周期。
在进行公差分析之前,我们需要对公差参数进行一些调整。首先,由于我们的用户定义的中频“us_zernike+msf.dll”曲面不是TEZI支持的曲面类型之一,所以必须删除曲面1的操作数,并将其替换为TPAR。
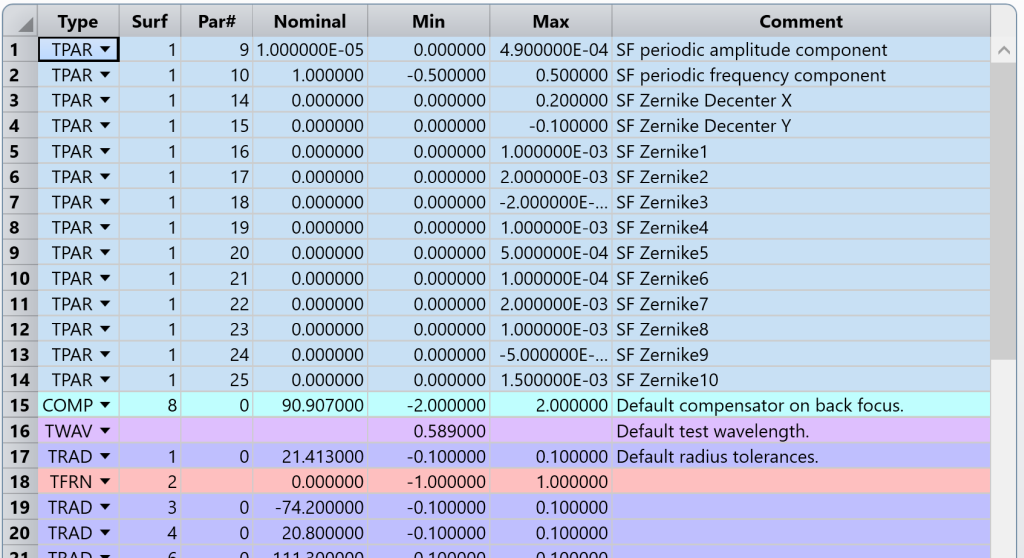
举例来说,TPAR(1,9)指表面1的第9个参数(振幅扰动)。同理,TPAR(1,10)表示表面1的第10个参数(周期扰动)。TPAR(1,16)到TPAR(1,25)是中频曲面的Zernike项,如编辑器中所示,名义值为零或非常小,并且随着蒙特卡罗分析的每次迭代而增加。
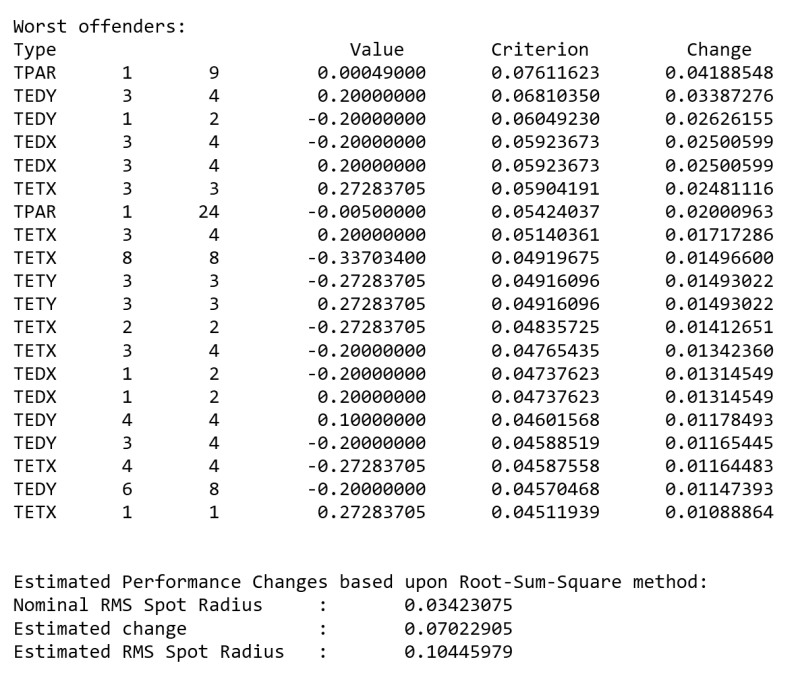
灵敏度分析表明,上述TPAR(1,9)是影响最严重的因素之一,说明表面波纹状不规则度的幅度越大,系统的性能下降越大。我们还可以看到基于平方根和的均方根光斑半径预估值。
以RMS光斑半径为标准,优化后焦长度,蒙特卡罗循环1000次。
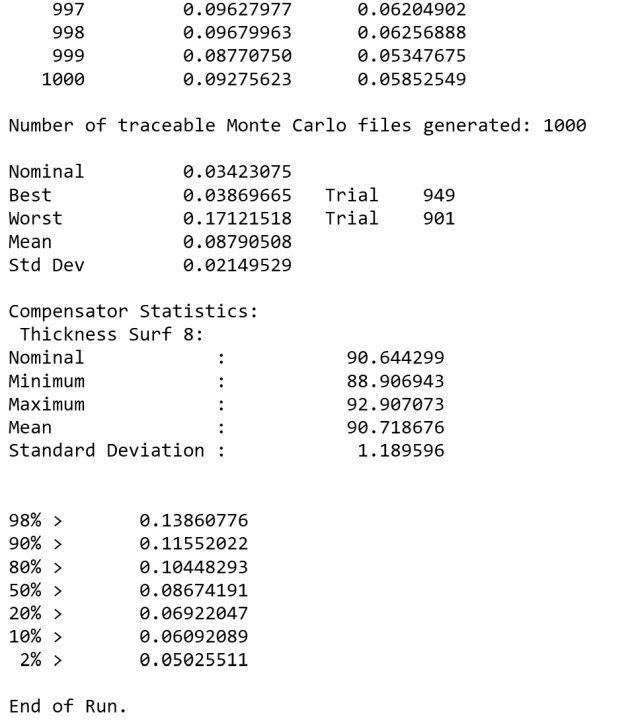
附件中提供的“MC_BEST.ZMX”和“MC_WORST.ZMX”可以用来检查。
我们可能会碰到获得性能较差结果的情况。所以,这要求我们的公差参数必须设置为合理的值,或者凭借经验得出的更好的参数方案。制造商也可能提供类似零件的性能表现信息,或者帮助预测最坏的结果,在确定设计方案前,这些信息是镜头设计过程中的关键。

注意事项

大部分面型都考虑了掠入射的情况,但是中频面型的周期部分没有考虑掠入射,所以有些情况可能无法提供准确的结果,比如一种广角物镜的第一个表面。此DLL将不适用于这种情况。
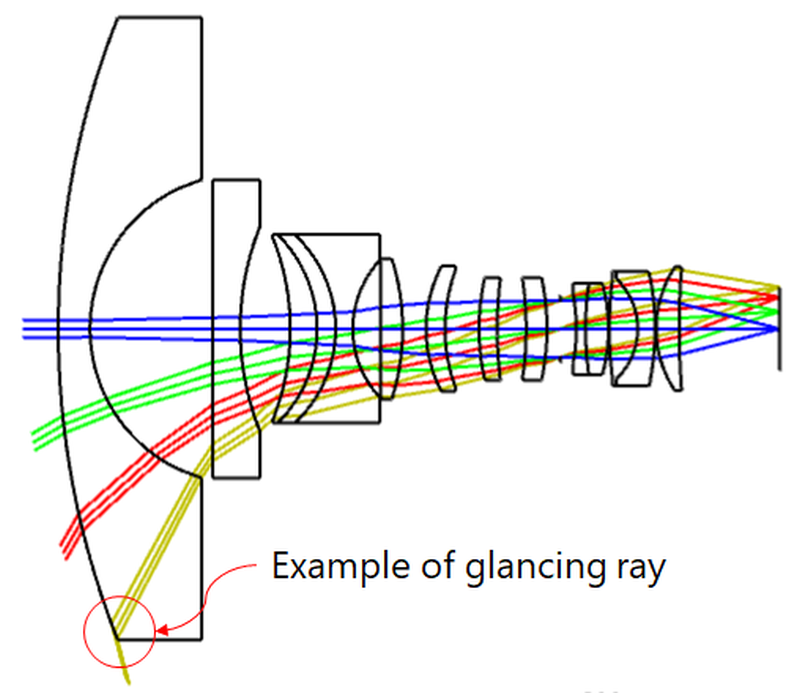
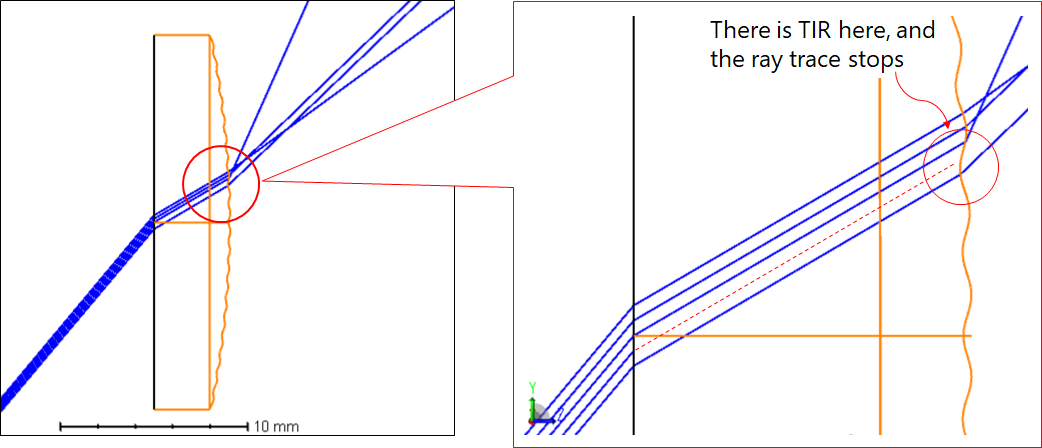
对于从高折射率材料到低折射率材料的表面,波纹表面上可能会发生全内反射 (TIR),从而使光线追迹停止。
周期非常小的不规则度(达到波长的大小量级时)计算可能不准确,因为该表面将无法考虑衍射效应。
对于模压塑料光学零件,形状上的 根切 (undercut) 是可以进行光线追迹的,但并不实际。

总结

我们研究了一种零件加工或模造上可能出现的同心加工误差和不规则度的建模方法。原理是将偶数非球面、Zernike多项式和周期函数结合,并编成用户定义的DLL,使其成为参数化表面(不同于CAD物体的非参数化表现形式)。使用周期分量作为参数实现了序列模式下的设计、仿真以及运行公差分析的能力。




