ProNas能量有限元方法在船舶中高频振动噪声分析预测的应用

安世亚太结构工程师
黄锦耀
摘要: 能量有限元方法是一种以能量密度为基本变量的数值计算方法,既能克服有限元(FEA)方法在中、高频分析时弯曲波在结构中传播,要求小尺寸网格引起计算效率低以及结构模态密集导致的频率上限的问题;又能改善统计能量法(SEA)丢失子系统空间特征信息的问题。本文以能量有限元理论为基础,建立船舶能量有限元计算模型,采用国产自主商用软件ProNas,对复杂激励下船舶各舱室产生的中高频结构噪声及空气噪声进行仿真计算,得到船舶各舱室声压级,并利用ProNas后处理功能显示激励源及传递路径处的能量分布云图。据此,对不满足噪声目标的舱室进行声学优化,最终解决了大型实际船舶工程的中高频振动噪声预测与控制问题。
关键词: 能量有限元;船舶;中高频振动噪声;ProNas软件;声学优化
1. 引言
1. 引言
结构中高频噪声的控制一直以来都是各工业领域研究的重点与难点问题,相比其它工业产品,船舶结构复杂、舱内环境更加独特[1]:船舶结构形式纵横交错,舱室众多,噪声诱因复杂,声源品种繁多密集,噪声强度较大;船舶结构中的振动噪声问题基本都在中高频范围;结构噪声与空气噪声可以相互转化。以上这些特点,使得船舶噪声控制起来十分困难。并且,国际海事组织(IMO)出于对船艇人员舒适性和健康的考虑,2014年签订生效的《船上噪声等级规则》,对船上振动和噪声指定了更严格的限制,与原有规则相比,要求居住区部分舱室声压级降低5dB(A),这就要求船舶工程设计人员需要采取更加有效的控制手段来降低船舶噪声。
目前,噪声预测的理论体系相对完善,并已将理论应用于大量实际工程中。按激励源频率及具体工业产品,可将振动和噪声的问题划分为低频、中频及高频。低频结构的响应具有确定性,工程中常用的数值方法有:有限元法(FEM)、边界元法(BEM);理论上,上述两种方法可计算任意结构、任意频率下的振动场。实际中,随着频率上限阈值增大,为了能准确反映结构的振动特性,通常需要划分单元的网格长度要远低于结构中弯曲波的波长;这样随着频率的增加,结构弯曲波波长变小,结构网格需要进一步细化,对计算资源要求变高;且中高频范围的结构模态密集,重叠交错,响应表现出不确定性,具有了统计的概念。因此,有限元和边界元就不再适合解决中高频问题。
近年来,统计能量分析(SEA)用于解决中高频问题,且模态越密集,其计算精度就越高。但统计能量分析不能保证子系统的空间变量信息的完整性[2],难以精确预示子系统内能量密度分布[3]且子系统的划分需要一定的经验,不易进行实际结构形态的设计与优化[4],模态密度及耦合因子的准确与否直接影响结果的准确度[5-6]。所以为了更好的控制中高频噪声,就需要有更好的理论方法。
能量有限元法[7](EFEA)是一种预测中高频动响应的新方法,它是以波动理论为基础,将结构离散化,在单元之间建立能量密度关系式,从而求解得到所有节点的能量密度;在实际计算中,节点个数较多,计算效率较低难度很大。ProNas能量有限元是在统计能量分析及能量有限元理论的基础上,以有限单元为研究对象,利用有限体积法及差分法推导出得类似于SEA的理论方程,联立求得每个有限单元的能量密度。本文着重介绍了ProNas能量有限元理论原理且应用ProNas商业软件对大型实际船舶的中高频噪声进行了仿真计算,求解得出船舶各舱室声压级。
2. ProNas能量有限元基本理论
2. ProNas能量有限元基本理论
ProNas能量有限元方法是在波动理论上建立的一种功率流方法,通过波动形式求解结构微元体运动方程,将波动形式下的动能密度、势能密度及功率流进行周期内时间平均和局部空间平均,得到能量密度与功率流的关系,代入稳态下能量平衡方程中可以得到能量密度控制方程;采用一定的数值离散方法对控制方程进行离散,得到能量有限元方程;在结构存在耦合的地方考虑波的反射和折射,求出耦合处能量密度与功率流的关系;最后进行总系数矩阵的组集,得到总体的方程,从而求出能量密度。
有限体积法的基础是将模型离散成若干个控制体,而这里的控制体可理解为有限元的 “单元”,ProNas能量有限元就是以单元为研究对象。
弹性介质中的能量平衡方程[8]如下,结构表面的能量流等于内部总能量的变化:
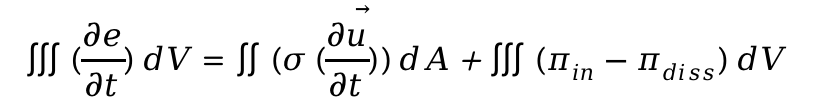
其中,e为能量密度;σ为结构的应力张量;![]() 为任一点的位移向量;
为任一点的位移向量;![]() 为输入的能量密度;
为输入的能量密度;![]() 为时间和空间的平均耗散的能量密度。
为时间和空间的平均耗散的能量密度。
由于结构内能量密度的变化是由于应力做功而产生,用应力核速度来表示,则能量密度的局部流出,即声强为[9]:
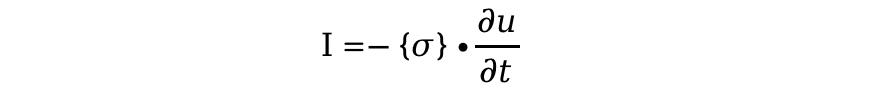
对于稳定响应,能量对时间的导数为零,子系统功率平衡,则:
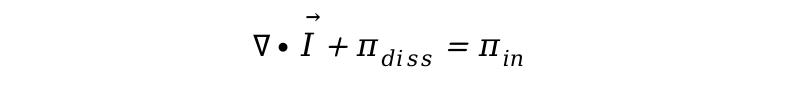
由于振动周期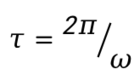 ,声能量密度和耗散功率之间的关系如下[10]:
,声能量密度和耗散功率之间的关系如下[10]:

并且,声能量密度和声强之间的关系如下:
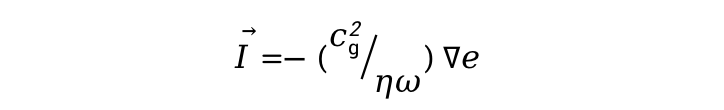
因此,可以得到能量密度方程:
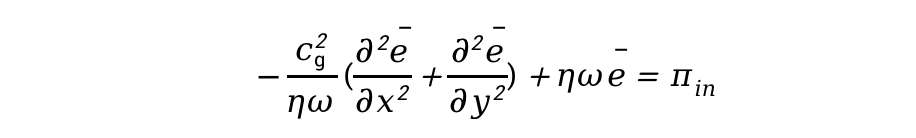
式中,![]() 为阻尼损耗因子;
为阻尼损耗因子;![]() 为群速度,
为群速度,![]() 为圆频率。
为圆频率。
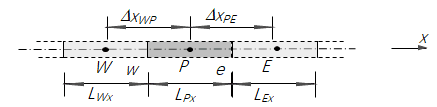
由于能量密度在材料变化、几何的改变(如截面面积、惯性矩)或结构的改变(如T节点、L节点)处产生了不连续的节点,针对这类耦合结构,传统的能量有限元方法的计算,需要引入耦合节点,并在每一个节点上完成能量守恒,如图1所示;而ProNas能量有限元法在耦合处建立了一种新的方法,引入控制体积,能量传递可以在控制体之间完成,如图2所示。
|
|
图1耦合处能量关系示意图 | 图2 ProNas能量传递 |
对于简单三段梁模型如图3所示:
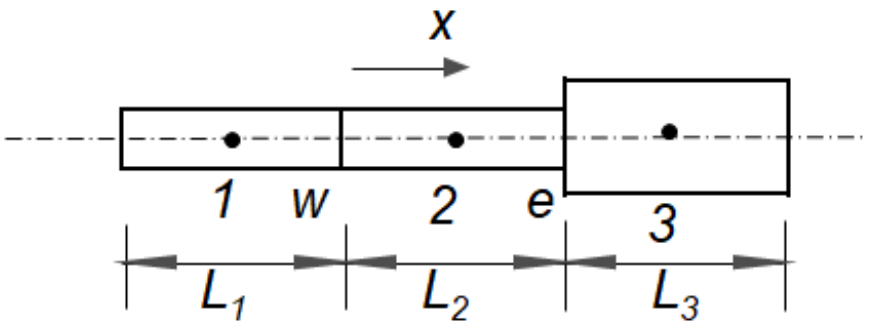 图3简单三段梁示意图
图3简单三段梁示意图
ProNas能量有限元方程如下:
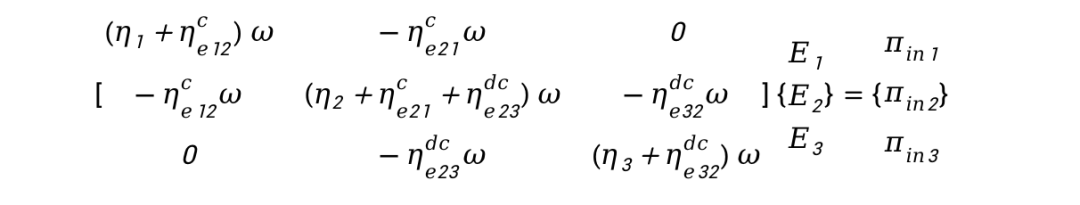
一般性地,矩阵方程可以表述为:
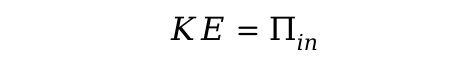
式中,K为总体能量密度系数矩阵;E为节点能量密度向量;![]() 为总体输入功率向量, 至此,ProNas能量有限元的能量密度矩阵方程,就可以写成与SEA方程结构形式一致的一次线性方程,易于求解。
为总体输入功率向量, 至此,ProNas能量有限元的能量密度矩阵方程,就可以写成与SEA方程结构形式一致的一次线性方程,易于求解。
3. 船舶模型建立
3. 船舶模型建立
3.1 船舶前处理模型
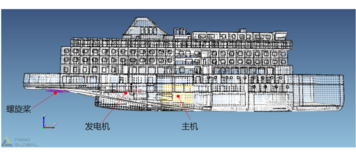
本文研究某大型客箱船,全长约200米,船宽约25米,采用的是双机双浆配置,主机为两台低速机,船的前部为载货区域,后部为居住区域和机械处所,利用成熟前处理软件对客箱船进行有限元划分。
因对居住区域及机械处所噪声控制要求较高,同时考虑计算时间成本,本案例对分析中高频噪声分析模型进行简化,只需截取局部模型,仅对居住区域和机械处所进行研究,结果如图4所示,模型共生成单元114358个,节点94357个。
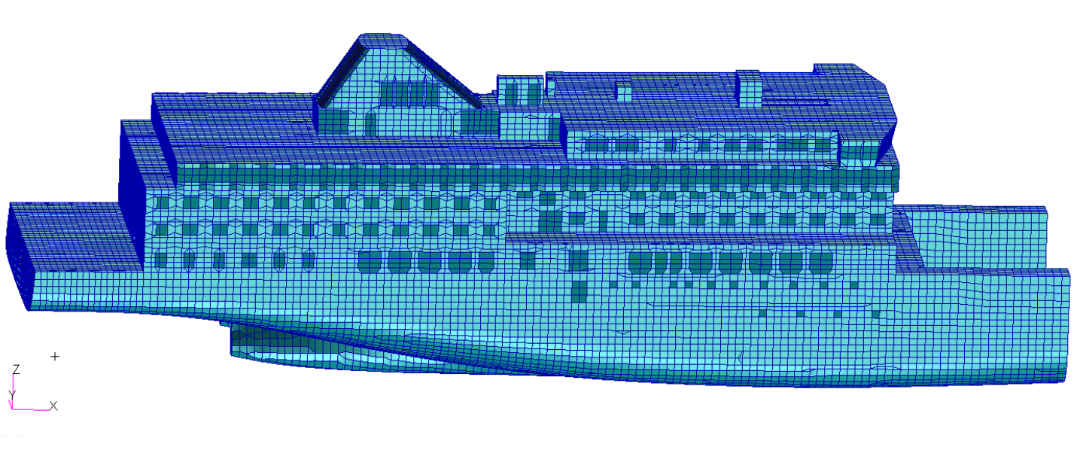
图4客箱船中高频噪声分析模型
3.2 ProNas软件模型处理
ProNas软件是国内知名公司安世亚太,联合国际上知名的噪声专家共同开发的中高频噪声仿真分析软件,是拥有国内自主软件著作权、自主可控的中高频软件,是能量有限元分析(EFEA)和统计能量分析(SEA)领域的代表性解决方案,代表着振动噪声工程界新一代的前沿技术。
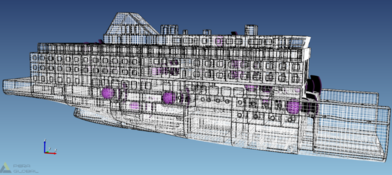
本案例利用ProNas声学仿真软件,分别对船舶的结构噪声与空气噪声进行了仿真计算。首先将Nastran格式的数据模型导入ProNas软件中,通过ProNas软件声腔自动识别功能自动划分声腔子系统,如图5所示。软件自动耦合声腔子系统和其临近贴合的结构单元,这样能量即可在结构单元与声腔子系统之间进行交换。然后对各舱室结构单元进行声学材料设置,如甲板敷料、绝缘布置材料,设置门窗材料等,如图6所示。

图5某客箱船声腔子系统

图6某客箱船声学材料施加
4.船舶模型激励输入
4.船舶模型激励输入
船舶的噪声源[11-13]主要包括主机噪声、螺旋桨噪声及水动力噪声,其中主机噪声和主螺旋桨又是重中之重。主机的干扰力包括惯性力、离心惯性力及倾复力矩,螺旋桨的激励力包括机械不平衡引起的干扰力、流场不均匀引起的叶频干扰力、伴流与空泡、轴承力和表面力。振动幅度的大小和激振力特性有密切关系,船体结构共振振动主要和干扰力频率特性有关,可以通过改变结构的刚性质量和阻尼,来使结构的固有频率移动,而受迫振动主要是物体在周期性外力作用下的响应。
根据主要噪声振动源的性能参数可以得到如表1所列激振力频率范围:
表1.激振力频率范围
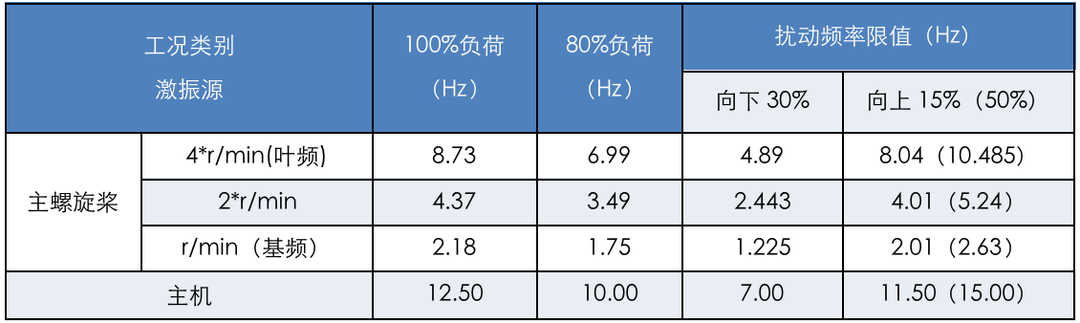
备注:考虑到频率储备和80%负荷为常用工况,以此为基数分别得到扰动频率的上下限值(Hz)。
本案例某客箱船模型,根据实际情况所受激励载荷主要有24个,分别为主机、螺旋桨、发电机、空压机、空调、风机等。其中主机、发电机、螺旋桨与船体作用,船体会振动产生结构噪声。其它激励源通过空气传递到船舶舱室内,产生空气噪声。结构噪声源在ProNas软件中分别在各设备的有限单元表面以速度级及加速度级的方式加载;空气噪声源分别在各激励源所在声腔子系统内以声功率级方式加载,如图7所示。
|
|
图7客箱船结构噪声、空气噪声载荷分布图 | |
5.船舶结构噪声及空气噪声分析结果与优化
5.船舶结构噪声及空气噪声分析结果与优化
5.1 船舶噪声分析结果
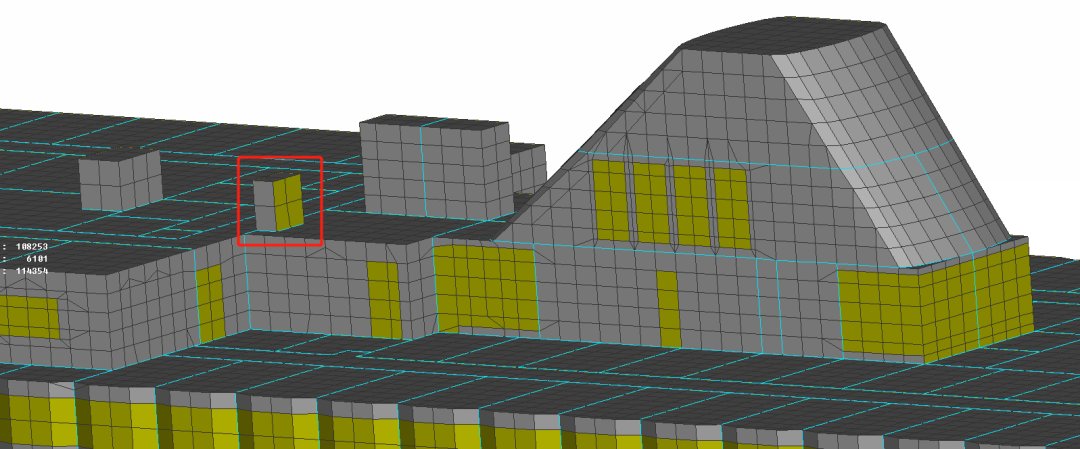
在倍频程中心频率63-8000Hz下分别将该客箱船结构噪声模型与空气噪声模型提交ProNas软件求解器,计算可得到各舱室声压级水平,图8分别为该客箱船在中心频率为500Hz时结构噪声仿真得到的结构速度云图与舱室声压云图。


图8结构速度云图、舱室声压云图(500Hz结构噪声)
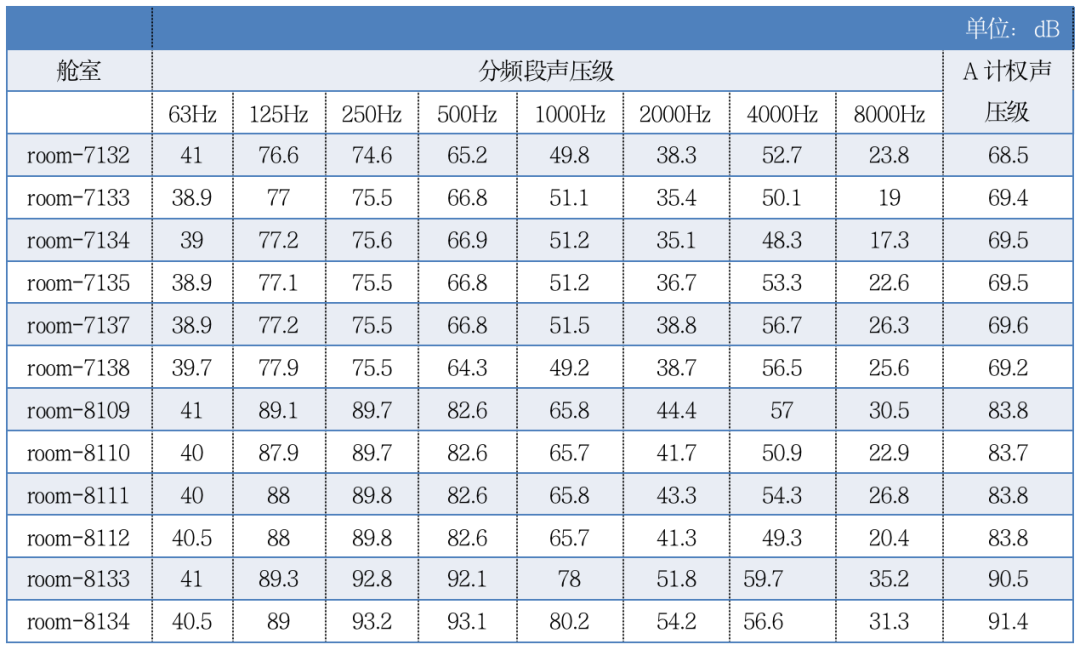
该客箱船舱室声压分析结果见表2,部分舱室声压级不满足目标值(55dB(A))。
表2.某客箱船舱室声压级(节选)
5.2优化方案
对于结构噪声超标的舱室,常用的优化方法为敷设阻尼。阻尼材料是将结构振动板的振 动能量快速转化为热能,从而减弱金属板的弯曲振动,阻尼材料通过这种方式可以有效地控制金属板的结构辐射噪声。通过云图分析可知,本案例结构噪声超标,多为主机与螺旋桨结构噪声引起。
由于该客箱船采用低速机,主机与船体钢板直接螺接,船体底部振动区域较大,且底部钢板厚度约为25mm-30mm,在实际应用中,阻尼层厚度一般要求为金属板厚度2-4倍,因此采用常规的在激励源附近敷设阻尼的方法,阻尼用量相对较大成本较高。并且,船舶结构复杂,结构噪声和空气噪声相互转化,因此常规阻尼敷设方法对超标舱室噪声控制效果一般。相比以上问题,本案例采用ProNas能量有限元法可精确、直观显示传递路径处能量分布,实现在不达标舱室处直接敷设阻尼,采用这种敷设方法,阻尼用量及成本在可控范围内,且噪声控制效果显著。
对于空气噪声不达标舱室,结合ProNas软件后处理结果云图,采用以下优化方案:
1) 部分娱乐室及放映室等地面浮动地板均改为50mm岩棉+钢板+阻尼+钢板型,再在上侧加10mm流平甲板敷料。
2) 部分甲板厨房抽风机室的内部,艉、中、艏面增加4mm钢板做成双墙舱壁,形成密封夹层空间,两层钢壁都设阻尼涂料。
3) 甲板房间合计26处所的天花板需穿孔(穿孔面向室内),孔径按1.8mm。壁板不 穿孔。
4) 在部分甲板机舱棚两侧直接面向公共处所和房间的舱壁,在外侧增加4mm压筋板做成的舱壁,形成密封的夹层空间,夹层内设50mm隔音棉。
5) 部分甲板均设 9mm 厚阻尼涂料处理。
5.3实船仿真与测试结果对比
经过多轮仿真计算以及方案优化,最终确定的整船噪声控制效果较好,并将优化方案应用到实船设计中,大多舱室噪声数值满足设计要求,对该客箱船实船舱室进行了噪声测试,如表3所示。
表3.部分舱室仿真结果与测试结果(节选)
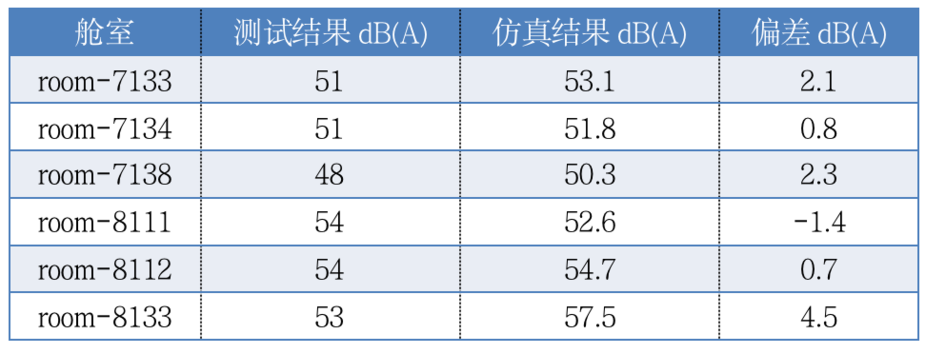
结果对比发现:room-8133房间偏差较大。分析原因为8133房间,模型前处理时的网格尺寸相对房间尺寸设置较大,房间的6个壁面都只离散成了一个网格,平均样本过少导致误差偏大。虽然ProNas能量有限元方法对网格的要求很低,模型不同的网格大小对声学结果影响较小。但是此方法计算舱室内部声压时采用了类似于统计能量对子系统的平均,需要对网格进行能量平均。
针对上述问题,在原分析模型基础上只对房间room-8133的各壁面网格重新划分,模型优化方案及结果如下表4所示;保证在每个壁面上能有多个单元等效,重新获得房间的仿真结果为56.3dB(A),与测试结果的偏差为3.3dB(A),两种模型对比的误差减小。因此,采用ProNas能量有限元方法计算舱室声压时,保证声学计算结果具有统计平均的意义,建议模型网格设置不宜过大。在此基础上作者也讨论了,基于上述细化的网格继续增多房间壁面上的等效网格数,发现房间8133的声压结果保持在56.3dB(A)不变,也证实了ProNas中高频声学求解器的准确性、可靠性。
表4. room-8133模型方案对比
room-8133 原模型 | 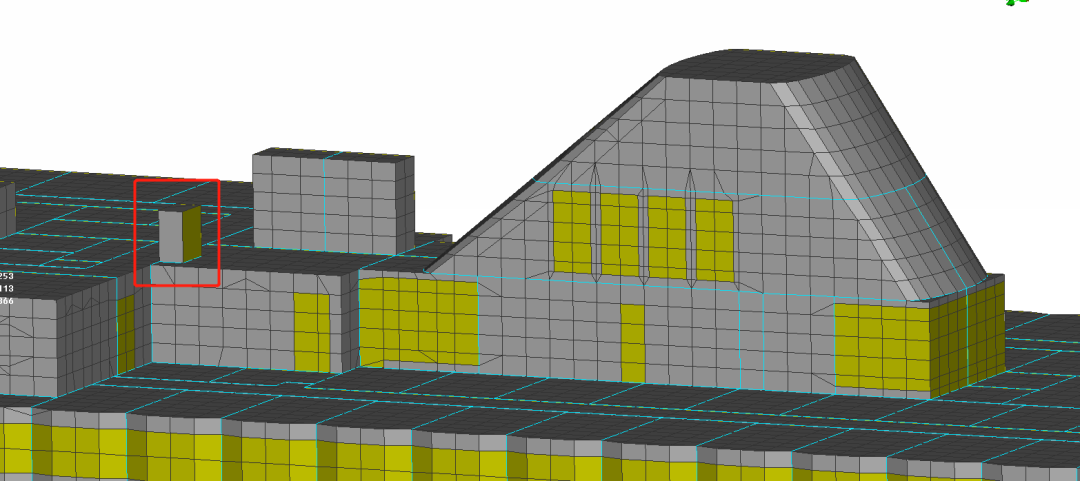 | 57.5dB (A) |
room-8133 优化模型 |
| 56.3dB (A) |
room-8133 对比模型 |
| 56.3dB (A) |
6. 结论
6. 结论
本文简要介绍了ProNas能量有限元方法,在此基础上应用ProNas软件建立了某客箱船声学模型,进行了整船的结构噪声与空气噪声仿真计算,对噪声不达标舱室进行仿真优化,并与实船测试结果进行对比,得出了以下结论:
1) ProNas能量有限元方法是一种用于预测和解决船舶及其它工业产品中高频噪声的可行性及有效性方法,具有很大的理论意义与现实价值。
2) 采用ProNas能量有限元方法,可避免常规中高频方法子系统建模操作的复杂性与专业性,提高仿真计算精度。
3) ProNas能量有限元方法不需要判断子系统模态密度,不需要确定系统之间的耦合因子,既保证模型的完整性,又提高仿真的时效性。
4) ProNas软件为解决中高频噪声提供了新的方法,为改进船舶设计参数提供了科学依据,提高了船舶的噪声设计质量,缩短研发周期,节约开发成本。
5) ProNas软件仿真得到的船舶结果与实测结果的最大误差值的绝对值在 5dB(A)内,满足模型的预测精度。
参考文献
[1] 陈小剑. 船舶噪声控制技术[M].上海:上海交通大学出版社, 2012:12-107.
[2] 林志立. 能量有限元法的模型及其在车身中的应用[D]. 中国科学院大学博士论文, 2018,宁波.
[3] 原凯,王建民,韩丽,等. 能量有限元在振动与噪声预示中的研究进展[J]. 强度与环境, 2015.42(3): 12-19.
[4] 祝丹晖,解妙霞,孔祥杰,等.复杂机械结构中高频动响应能量有限元方法研究[J]. 中国工程科学,2013,15(1): 107-112.
[5] 庞剑,谌刚,何华. 汽车噪声与振动----理论与应用[M]. 北京:北京理工大学出版社,2005: 54-62.
[6] 陈书明,王登峰,马一功,等. 模态密度计算精度对车内噪声预测精度的影响[J]. 吉林大学学报,2010,40(2): 335-340.
[7] 孙丽萍,聂武. 能量有限元法在船舶结构中的应用[J]. 哈尔滨工业大学学报,2008,40(9): 1491-1494.
[8] BERNHARD R J. The family of EFA equations and their relationship to SEA[C]//Proceedings International Conference Noise and Vibration Energy Methods.Lyon:[s.n.] 2000:248-257.
[9] BERNHARD R J, HUFF JE. Structural-acoustic design at high frequency using the energy finite element method[J]. Vibrational Acoustics, 1999, 121(1):295 -301.
[10] MOENSI, VANDEPITTED, SASP. Study of the applicability of energy finite element method for plates [C] // Proceedings International Conference Noise and Vibration Energy Methods. Lyon, France: [s.n.], 2000: 312 -323.
[11] 翁长俭. 船体振动学 [M]. 大连:大连海运学院出版社,1992.
[12] 邱斌. 高速船全频段舱室噪声预报与控制方法的研究 [D]. 武汉理工大学硕士学位论文,2010,武汉.
[13]李峰,徐芹亮,腾瑶,张菁.统计能量法在船舶噪声与振动控制中的应用[J].噪声与振动控制, 2011.12(6): 152-155.