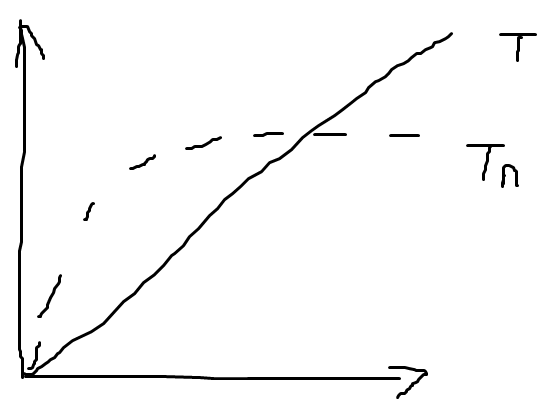
浮体运动固有周期
本文摘要(由AI生成):
本文主要讨论大型浮体的刚体运动固有周期,包括六个运动自由度、刚度、质量、固有周期等概念。刚度由静水力和系泊系统提供,质量包括浮体自身质量和附加质量。固有周期由质量、刚度和附加质量决定,求解过程需要考虑附加质量随周期变化的情况。
本文仅对大型浮体的刚体运动固有周期展开讨论。
基本假设
1.认为浮体是刚体,不考虑其变形与水体的相互作用。
2.认为刚度变化是近似线性的。
3.认为浮体运动是近似线性的。
六个运动自由度
浮体一般认为有六个运动自由度,纵荡、横荡、升沉、横摇、纵摇和艏摇,这六个自由度组成6X6的矩阵,其中纵荡、升沉、纵摇耦合,横荡、横摇、升沉耦合。
刚度
刚度,或者是回复力/恢复刚度,通常由两种方式来提供:静水力和系泊系统,这两部分组成6X6的刚度矩阵,这里仅关注矩阵的主对角线值。对于没有系泊系统的浮体,其回复刚度仅由静水力提供:升沉由浮体水线面特性决定,横摇由横稳性决定,纵摇由纵稳性决定,这三者组成刚度矩阵对角线3、4、5刚度值。系泊系统可以组成另外三个运动自由度主元素值。
质量
浮体质量矩阵为6X6,一般而言主对角线元素影响最大。质量矩阵包括两部分:浮体自身质量/惯性质量(自行计算),浮体附加质量/附加惯性质量(程序计算)。
固有周期
不考虑耦合状态下,浮体单自由度运动固有周期 Tn=2π[(M+△M)/K]^0.5,M为对应自由度
质量/惯性质量,△M对应自由度的附加质量/附加惯性质量,K为对应自由度的刚度。(严格的说阻尼的影响也应该考虑,但一般情况下可以认为浮体运动的阻尼足够小,可以忽略)。
附加质量本质上是关于水质点加速度的力,因为与加速度相关所以是惯性力,其与水质点的运动特性密切相关,是浮体受迫运动产生的,是关于周期T而与波浪方向无关的值。
由于附加质量同周期T相关,所以当T变化的时候,附加质量会发生变化。(严格的说应该是低周期条件下,附加质量随着周期变化而变化,当周期逐渐拉长,附加质量会趋于一个定值,即低频附加质量)。
所以,固有周期Tn的求解是一个过程。当周期T变化时,△M发生变化,Tn也发生变化,当Tn=T的时候,T即为该自由度的固有周期。