手算二维稳态热传导
手撸一个简单的二维稳态热传导问题。
注:案例取自《The Finite Volume Method in Computational Fluid Dynamics》,F.Moukalled。公式显示不全时可左右滑动公式。
”
1 问题
如图所示,考虑一个由两种材料构成的二维矩形区域内的热传导过程。
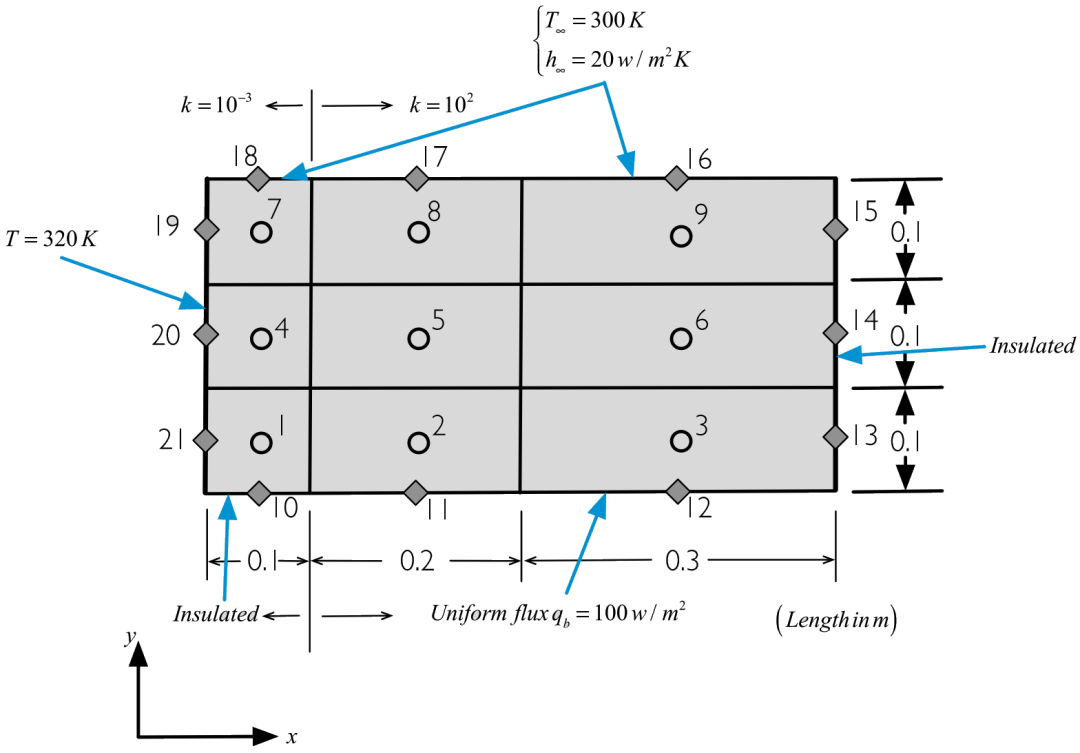
控制方程为:
式中, 为温度。
针对图中所示的热导率(k)和边界条件:
推导图中所示的所有单元的代数方程。 求解方程组并计算格单元的温度值。 计算底部、右侧和顶部边界上温度值。 计算通过顶部、底部和左侧的净传热量,并检查是否满足能量守恒定律。
2 求解
2.1 基础数据
模型单元及及节点编号如图所示。
各单元形心点坐标为:
节点距离为:
单元尺寸为:
单元体积为:
单元面数据插值因子(对于正交笛卡尔网格,体积加权与距离加权等同):
区域上的热导率:
跨材料界面的热导率采用调和平均计算:
2.2 单元1
计算系数:
界面热导率:
单元1的西侧与南侧皆为边界,离散方程的一般形式可写成:
方程系数:
西侧系数和南侧系数没有出现在方程中,因为它们的影响通过边界条件影响源项。
因此系数:
可得到单元2的离散方程:
2.3 单元2
计算系数:
界面热导率:
离散方程可写成(单元2的南侧为壁面):
其中:
单元2的南侧面为诺依曼边界条件,直接给定热通量的值。因此:
离散方程的其他系数为:
因此,单元2的离散代数方程为:
2.4 单元3
单元3的东侧与南侧为边界。
计算系数:
界面热导率:
单元3离散方程的一般形式为:
其中:
东侧边界为绝热,南侧边界直接给定热通量,因此:
计算离散方程的系数:
因此单元3的离散代数方程为:
2.5 单元4
单元4的左侧为边界。
系数计算:
界面热导率:
离散方程:
其中:
西侧面边界为温度边界,其系数及源项为:
则有:
单元4的离散方程为:
2.6 单元5
单元5为内部节点,不与任何边界相邻。
系数计算:
界面热导率:
离散方程:
方程系数:
得到离散方程:
2.7 单元6
系数计算:
界面热导率:
离散方程为:
方程系数:
单元6的右侧为绝热边界。
因此代数方程为:
2.8 单元7
单元7的西侧为恒温边界,北侧为对流换热边界。
系数计算:
界面热导率:
离散方程写成:
式中系数:
西侧与北侧系数不出现在离散方程中。
有:
因此离散方程系数:
代数方程为:
2.9 单元8
单元8的北侧为对流换热边界。
系数计算:
界面热导率:
离散方程的形式为:
其中:
边界处理:
因此方程系数:
可得到代数方程:
2.10 单元9
计算系数:
界面热导率:
离散方程的形式为:
单元9的东侧与北侧为边界,相关计算:
得到方程的系数:
得到代数方程为:
2.11 代数方程
组合所有单元的方程,可得到系统方程组:
可以写成矩阵方程的形式:
可以使用程序求解矩阵方程:
import numpy as np
A = [
[0.005,-0.002,0,-0.001,0,0,0,0,0],
[-0.002,240.002,-40,0,-200,0,0,0,0],
[0,-40,340,0,0,-300,0,0,0],
[-0.001,0,0,0.006,-0.002,0,-0.001,0,0],
[0,-200,0,-0.002,440.002,-40,0,-200,0],
[0,0,-300,0,-40,640,0,0,-300],
[0,0,0,-0.001,0,0,0.006998,-0.002,0],
[0,0,0,0,-200,0,-0.002,243.962,-40],
[0,0,0,0,0,-300,0,-40,345.9406]
]
B = np.array([0.64,20,30,0.64,0,0,1.2394,1188.12,1782.18]).reshape(-1,1)
T = np.linalg.solve(A,B)
得到各单元的温度值:
上面的计算过程很容易转换为程序。也可以加密网格进行计算,处理方式完全相同。
3 其他计算
3.1 底部边界的温度
底部边界的温度值可以通过指定的边界条件计算得到。底部边界为绝热及热通量边界,均属于诺依曼边界条件。
对于绝热边界,
3.2 右侧边界的温度值
右侧边界为绝热边界。
因此边界温度值为:
3.3 顶部边界的温度值
顶部边界为对流换热边界,温度值可通过公式计算:
代入参数可得到:
3.4 左侧边界上的总传热量
可以通过下式计算:
3.5 顶部边界总传热量
计算为:
3.6 底部边界的总传热量
底部已知热通量,可以利用热通量直接乘以面积得到传热量:
3.7 检查能量守恒
计算区域内的流入流出的热量之和。
增加网格密度及在计算过程中保留更多的有效数字能够提高计算精度。
(完)





