非线性有限元分析之超弹模型Mooney-Rivlin
本文摘要(由AI生成):
本文介绍了Mooney-Rivlin超弹模型,它是高分子材料力学中常用的模型之一。Mooney-Rivlin模型根据阶数高低有2参数、3参数、5参数和9参数应变能等多种形式,可以模拟不同复杂程度的应力-应变曲线。高阶模型能更准确地描述材料行为,但也需要更多的计算量和参数拟合。在实际应用中,应根据材料实验的应力-应变曲线选择合适的模型,并满足正定性要求以保证求解收敛。Mooney-Rivlin模型在小应变范围内得到了广泛应用,但在大应变、可压缩超弹材料等方面存在局限性。本文还通过一个压缩状态分析的例子,展示了如何在非线性有限元分析中使用5参数Mooney-Rivlin模型。
在之前的几篇文章中,我们介绍了非线性有限元分析中的超弹模型,同时也详细介绍了Arruda-Boyce和neo-Hookean两个经典模型。今天我们就来介绍另一个经典的超弹模型:Mooney-Rivlin。
Mooney-Rivlin分别以两位力学家M. Mooney和R. S. Rivlin的姓氏组合来命名。1940 年,Mooney在著名的Journal of Applied Physics期刊发表一篇名为A theory of large elastic deformation的论文,8年后的1948年,Rivlin在Philosophical Transactions of the Royal Society of London期刊上发表了名为Large elastic deformations of isotropic materials的文章。于是就有了今天的Mooney-Rivlin模型,曾一度统领橡胶力学研究的整壁江山。同时,也为其他以应变张量不变量(invariant)为核心的模型奠定了基础。另一类超弹模型是以主拉伸(principal stretches)为核心的模型,如Ogden模型,我们会在以后的文章中介绍到。

1893年,Mooney出生于美国密苏里州的堪萨斯城,24岁时获得密苏里大学的本科学位,30岁时获得芝加哥大学的博士学位。曾是美国国家研究委员会的的会士(National Research Council Fellow),也曾经在西部电气公司和美国橡胶公司担任物理学家。和我们之前介绍的Rivlin一样,Mooney博士将一生的工作和研究都贡献给了高分子材料力学。当然Mooney要比Rivlin年长个20多岁。关于Rivlin博士已经在上一篇文章中有介绍,这里就不再赘述了。
和其他超弹模型一样,我们用弹性应变能来表征力学性能。Mooney-Rivlin根据阶数高低,常见的有4种:2参数,3参数,5参数,和9参数应变能。
Mooney-Rivlin 2参数的弹性应变能为:

Mooney-Rivlin 3参数的弹性应变能为:

Mooney-Rivlin 5参数的弹性应变能为:
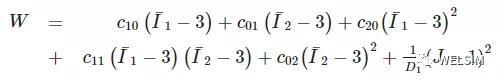
Mooney-Rivlin 9参数的弹性应变能为:
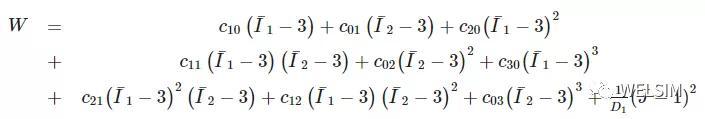
从上面的4个弹性应变能公式可以看出:
高阶数的应变能模型可以模拟更加复杂的应力-应变曲线,但也意味着需要更多的计算量,实验,以及参数拟合。同时增加了非线性求解器的负担,可能会导致更难收敛。
Mooney-Rivlin模型是多项式(Polynomial)模型的特殊形式。当N=1时,多项式模型缩减为2参数Mooney-Rivlin,当N=2时,多项式模型缩减为5参数Mooney-Rivlin;当N=3时,多项式模型缩减为9参数Mooney-Rivlin。
2参数模型中,当参数C01为零时,简化为Neo-Hookean模型(C10系数2倍关系)。非零的C01项使得单轴拉伸受力下的变形预测更为准确,但该模型还不能准确模拟多轴受力数据。或者由某种变形试验得到的数据,不能用来预测其它类型的变形。
2参数模型的剪切模量为定常系数\mu=2(C10+C01),不适合用来模拟炭黑填料硫化橡胶。C10和C01均为正定常数。对于大多数橡胶,C10/C01≈0.1~0.2时,在应变150%以内可得合理的近似。
三项或多项Mooney-Rivlin模型可以描述非定常剪切模量。然而,引入高次项后需小心计算,因其可能会产生不稳定应变能值,得到超出试验范围的非物理结果。
应变能函数的选用与正定性
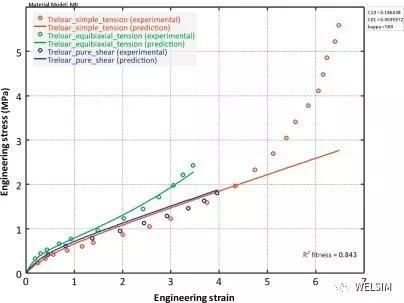
这四种函数的Mooney-Rivlin模型实际仿真中应该选用哪个呢?往往根据材料实验的应力-应变曲线来确定。如单曲率(没有拐点)应力应变曲线,可以使用2或3参数。双曲率(含有一个拐点)可以使用5参数。三曲率(含有2个拐点)可需选用9参数模型。
同时为了产生有效且正确的超弹材料特性,Mooney-Rivlin参数须满足特定的正定性要求。如不能满足这些约束条件,可能导致求解无法收敛。对于不同参数的Mooney-Rivlin,满足正定性的参数约束要求如图所示。
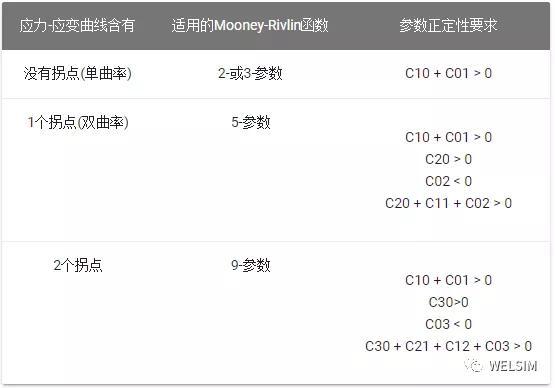
总体来说,Mooney-Rivlin模型得到了广泛的认可和应用。尤其是在小应变范围内(0~100%拉伸和30%压缩)能够较好的表征橡胶材料的力学行为。不同参数的模型也提供给用户针对不同工况更多的选择。然而,Mooney-Rivlin也有一些局限性:
不适合用于变形超过150%的工况。
高阶Mooney-Rivlin由于参数较多,参数相对比较难从手册或文献中获得,需要通过对实验数据的曲线拟合来得到。
不适用于可压缩超弹材料,如泡沫材料的分析。
对所输入数据范围以外的实验数据的预测误差较大。
Mooney-Rivlin超弹模型的非线性有限元分析
本例中,我们将使用5参数Mooney-Rivlin对橡胶材料的压缩状态进行分析。
定义Mooney-Rivlin超弹材料
这里我们模拟橡胶材料,并输入参数为:C10=-0.55 MPa, C01=0.7 MPa, C20=1.7 MPa, C11=2.5 MPa, C02=-0.9 MPa, D1=0.001 MPa^-1。
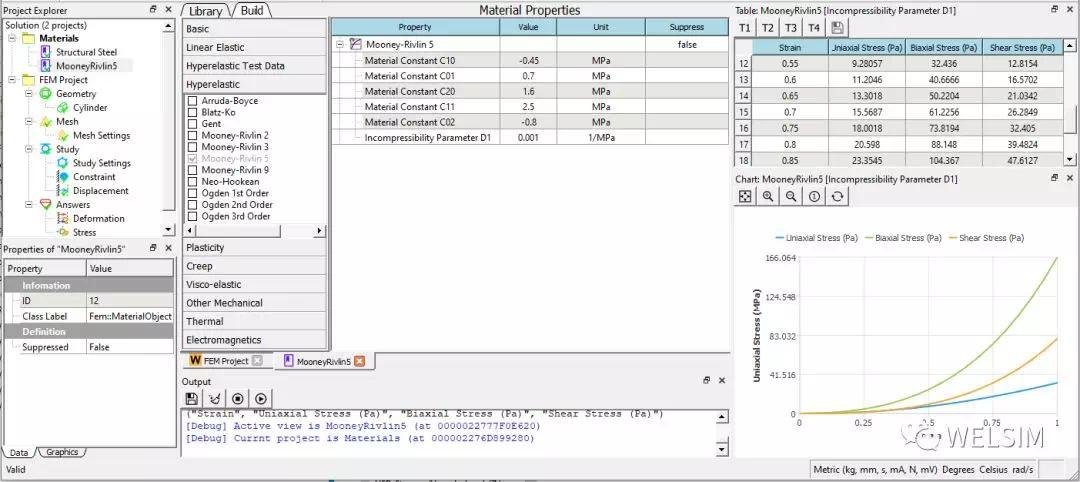
建立模型
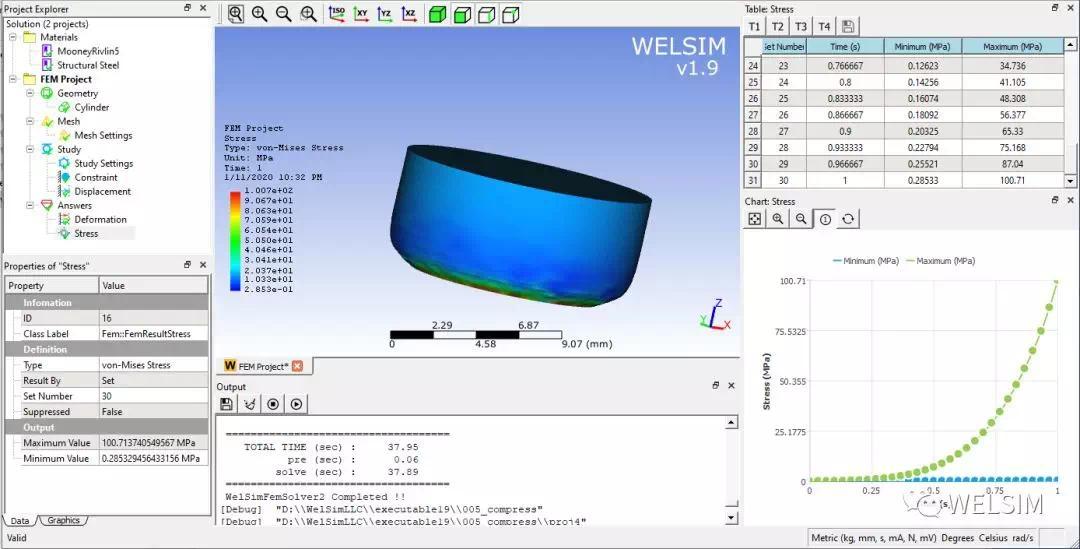
建立一个直径为10mm,高为10mm的圆柱体。划分网格。固定底部约束。并对顶部面施加向下5mm的位移。
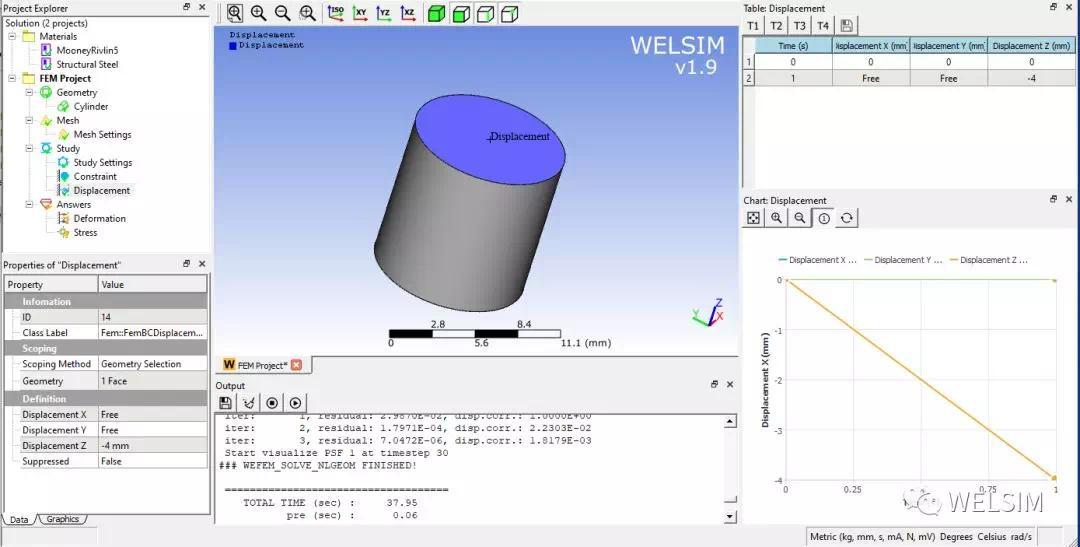
求解
由于非线性较强,我们设置30个子步。并点击求解按钮。
查看结果
等效应力分布如图所示。可以发现在等步位移工况下,应力呈非线性分布递增。