基本工程问题是否需要前沿几何理论?
2020年初,又到了回顾过去展望未来的时候。这些年来,我们团队一直秉持初心,将现代几何拓扑理论推广到计算机科学范畴,应用于工程和医疗领域。我们认为,很多工程领域最为基本的问题,尤其是多年来被工程师们瞩目但又没有实质性突破的开放问题,其背后都有非常深刻的几何或者拓扑理论。工程问题长期停滞不前的根本原因在于工程师们没有从理论层面彻底理解问题的本质,而是试图用工程的思维习惯和方法来解决。最终我们必须用前沿、现代的理论来加以阐释,从而找到工程上的解决方法。
2019年,我们坚持用最优传输理论来理解对抗生成网络(GAN),特别是用蒙日-安培方程的正则性理论来解释模式崩溃问题(mode collapse);我们用复纤维丛的示性类理论来解释计算机辅助设计中四边形网格奇异点构型问题;同时用共形几何将拓扑优化从欧氏空间推广到弯曲流形上面。
深度学习和最优传输
2019年,深度学习依然狂飙突进,与应用层面相比理论进展严重滞后。我们与丘成桐先生长期密切合作,利用最优传输和蒙日-安培方程理论来理解生成模型。我们认为深度学习成功的内在原因在于这种方法能够抓住大数据的本质,大数据的本质模式可以概括为如下的物理定则(physics law):一类自然数据可以被视作嵌入在高维空间中的低维流形上的概率分布。深度学习具有两个主要任务:一是学习流形结构,表示为编码和解码映射,流形的参数空间就是隐空间或者特征空间;二是概率分布变换,即将白噪声变换成数据分布。深度神经网络的唯一功能就是表达欧式空间之间的连续映射,因此在统计深度学习领域,所有的数据都被表示成映射,概率分布也被表示成映射,即从白噪声到给定概率分布间的传输变换(transportation map)。由此,统计深度学习可以由范畴语言来表述,其范畴为{流形上的概率分布,流形间的映射}。
学习流形结构本质是拟合编码(encoding)和解码(decoding)映射,可以用经典的函数逼近理论来理解,特别是Kolmogorov和Arnold的定理:任意连续函数
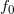
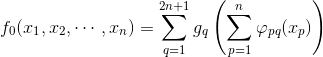

概率分布变换可以由经典的最优传输理论来解释:任意两个概率分布之间存在最优传输变换,其传输代价定义了分布之间的Wasserstein距离。GAN的生成器本质上就是计算最优传输变换,生成器计算Wasserstein距离。由Brenier理论,最优传输映射是Brenier势能函数的梯度映射,Brenier势能函数满足经典的蒙日-安培方程(Monge-Ampere):
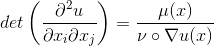
由凸微分几何中的Minkowski和Alexandroff理论,蒙日-安培方程归结为求解一类特殊的凸多面体。我们发展了基于变分原理的几何算法,将最优传输问题转化为凸优化问题,应用于GAN模型,从而使得黑箱变得透明。
GAN训练非常不稳定,收敛困难,对于超参数过于敏感。学习多模态(mode)的分布时,经常只学会部分模态,而丢失其他模态。强加了规则项后,GAN虽然覆盖了所有模态,但是会生成虚假的样本。这些现象被称为所谓的模式崩溃(Mode Collapsing)。模式崩溃是阻碍深度学习技术在实际应用中推广的主要障碍之一。由Brenier的极分解定理(Polar Decomposition), 所有的概率变换都可以被分解成最优传输映射与保测度自同胚的复合。由蒙日-安培方程正则性理论(例如汪徐家、Figali的工作),通常最优传输映射整体是非连续的。但是深度神经网络只能表示连续映射,这一本质矛盾揭示了模式崩溃的内在原因。

图1. 基于最优传输的几何方法生成的人脸图像。
例如我们用GAN来生成人脸图像。每张人脸图像被视作高维空间中的一个点,所有的人脸图像构成一个点云,分布在某个低维流形附近。我们用深度学习的方法将流形降维到隐空间,流形上点云的密度分布被映射成隐空间中的一个概率分布。我们在隐空间将白噪声用最优传输映射变换成数据的隐空间分布。最优传输映射的间断点集合对应着人脸图像流形的边缘,即貌似合理的人脸图像,但在现实生活中出现的概率为零。例如,我们所有的训练样本或者是黑色眼睛或者蓝色眼睛,用这种方法我们可以找到一只眼睛黑色另一只眼睛蓝色的人脸图像,它们位于人脸图像流形的边缘。

图2. 基于蒙日-安培方程正则性理论找到的人脸图像流形的边缘。
在2019年间,我们团队收到大量来自世界各地学者的电邮,询问最优传输理论和算法的细节,讨论在各种深度学习模型中的具体应用。也有很多学者给我们发来了感谢信,他们受到我们学说的启发,将最优传输应用于深度学习,发表在深度学习的顶级会议和期刊。前不久,在清华三亚数学论坛上,老顾遇到了湖南大学的黄教授与华南理工大学的谭教授。黄教授从事蒙日-安培方程、Minkowski问题的理论研究,谭教授研究最优传输理论在深度学习中的应用,他们在各自领域都取得了令人瞩目的成就。老顾和他们深入地探讨了相关的学术问题,再次感受到纯粹数学理论对于实际工程应用的指导,和工程实际要求对于纯粹理论研究的推动。似乎很少有如此深刻抽象的理论,在工程领域如此迅猛地传播。从会议中心可以眺望到三亚的知名景点-天涯海角,最优传输理论和深度学习令老顾天涯海角遇知音。
除了丘成桐先生的蒙日-安培方程理论之外,我们的工作中也用到了2010年菲尔兹奖得主Cédric Villani教授的最优传输理论成果和他的学生2018年菲尔兹奖得主Alessio Figalli教授的偏微分方程正则性理论成果。Villani教授在伦敦召开的New Frontiers in Mathematics 2018大会上介绍了我们的工作【1】。Figalli教授在波兰召开的DEA2019大会上(Dynamics,Equations and Applications)也引述了我们的工作【2】。数学大家的加入将会极大地推动人工智能理论的发展。
计算机辅助设计与纤维丛示性类
我们日常生活中所使用的几乎一切工具都是计算机辅助设计的产品,都被表示成所谓的样条曲面。例如简单的牙刷,由模具注塑成型,而金属模具先被表示成样条曲面,然后由数控机床加工出来。样条曲面设计的前提是曲面四边形网格生成,即将曲面剖分成四边形网格。四边形网格上拓扑度不等于四的顶点被称为是奇异点,奇异点的位置和拓扑度被称为是奇异点的构型。四边形网格生成的关键在于如何确定奇异点的构型,这是计算机辅助设计领域(CAD)最基本的问题之一。

图3. 曲面四边形网格剖分。
虽然CAD与人们日常生活息息相关,从业人员众多,CAD领域的研究历史悠久,但是这一基本问题一直没有得到根本解决。前人的研究主要注重曲面的拓扑结构,但是实际世界中所有的曲面都是黎曼面,都具有共形结构,因此我们认为这一问题的本质在于共形几何。我们最终用复线丛的示性类理论解决了这一问题。我们证明了每个四边形网格都等价于黎曼面上的亚纯四次微分,可以视作黎曼面全纯余切丛四次幂的一个截面,而四边形网格的奇异点(构型)可以被视为这一全纯线丛的示性类。因此,不同
四边形网格奇异点的构型彼此等价,即相差一个主除子(某个全局亚纯函数的除子),因而在Abel-Jacobi映射下,主除子被映到Jacobi簇的零点。
我们终日被工业设计的产品围绕,却又无法参透几何设计的基本问题,四边形网格奇异点构型,这令我们困扰多年。虽然我们可以选择无视而与之相安无事,或者等待他人斟破其中奥妙,但是总是无法忍受思想的混沌。当我们看透这个问题本质的时候,我们发现其深度远非初等,如果不用复线丛的示性类理论,无法将问题解决。或许这是迄今为止复线丛丛示性类理论在计算机科学领域中的第一个深刻应用。
作为陈省身先生学派的弟子,我们对于矢量丛示性类理论耳熟能详,但是我们原来对于这一理论的理解过于肤浅,也从来没有想象到陈类理论居然可以用于解决机械设计领域最为基本的问题。在计算机科学领域,也没有应用复线丛理论的先例。虽然工程师们依照直觉发明了样条理论,并且将其发展成现代工业基础,从汽车制造到航空航天,从数控机床到日常用品,我们几乎时刻依赖于样条理论的成果,但是其理论根基并不完美。广大工程设计人员的日常设计工作中,依然强烈依赖于人的灵性来手工弥补理论的缺陷,人们对此习以为常,并且将这种手工技巧视为“绝活儿”。示性类理论将这种绝活转化为严格的算法,用自然铁律取代了手工的灵性。
拓扑优化和共形几何
在2019年,我们团队和陈士魁教授的团队将拓扑优化方法系统地从欧几里得平面推广到带有黎曼度量的曲面上面。依随三维打印技术的蓬勃发展,拓扑优化日益成为机械设计领域的热点。拓扑优化方法在设计空间中优化材料的布局,在满足给定机械力学条件的限制下,使得系统性能达到最优。例如在汽车设计中,在保证安全性的前提下,如何优化汽车零部件使得车身重量减轻,以达到省油的目的,其关键技术在于拓扑优化。
拓扑优化可以被描述成一个变分问题,其材料的分布密度函数为未知函数,满足特定的偏微分方程和积分不等式,优化目标是某个能量泛函。传统的拓扑优化方法归结为在欧几里得空间求解微分方程,例如用有限元方法或者水平集方法。但是工业实践中,机械设计的部件往往是弯曲的曲面,这需要我们将拓扑优化方法从平面推广到曲面,从欧氏空间推广到黎曼流形。等价的,我们需要将传统的微分算子推广成黎曼度量下的协变微分算子。
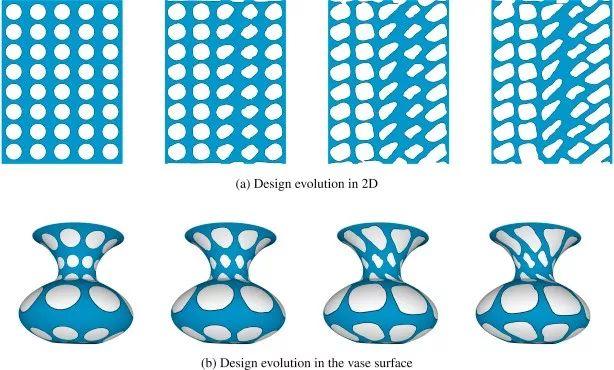
图4. 曲面上的拓扑优化。
共形几何可以将所有带黎曼度量的曲面保角映射到平面区域,将黎曼度量转化为一个标量函数,协变微分算子具有最为简洁的形式,从而可以直接将传统拓扑优化方法推广到曲面上。如图4所示,我们用拓扑优化方法来设计一个花瓶的加强筋结构,用共形映射,我们将曲面映射到平面区域,在平面上求解微分方程。
这种方法适用于所有的曲面壳层结构,微分算子自动转化,理论完备,算法高效,具有很大潜力应用于工业实践之中。
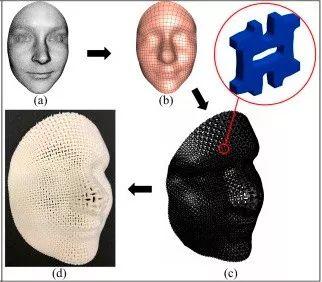
图5. 超材料曲面设计。
同样的方法也适用于曲面上的超材料设计。超材料设计首先设计每个单元的几何结构,然后周期性重复这种单元,组装成整体材料。超材料具有特殊的力学性质,这些性质自然界材料无法具备。传统的超材料都是在欧氏空间中设计。通过共形几何我们可以构造超材料曲面。图5显示的是由一个二维负泊松比超材料构成的人脸曲面。
宏观上的热力学现象可以由微观上的布朗运动来解释。共形变换保持布朗运动,因此拉普拉斯方程、泊松方程是共形不变的。因此,曲面上的热传导问题可以借助共形映射归结为平面上热传导问题。由此可见,在工程领域,任何在平面区域上运行的方法都可以通过共形几何方法推广到带有黎曼度量的曲面上面,这一规律是普适的。
感想
2019年的最大感受就是为了解决工程领域的基本问题,我们必须使用先进的几何拓扑理论。在工程领域,人们为了解决生产实践问题,采用大量的经验性方法,发展出各种虽不严密但又确有实效的算法,在社会中得到广泛应用。但是为了证明这些方法的严密性,所需要的理论工具并不在目前的工程科学范畴内,需要引入新的数学概念和理论。一方面对于工程背景的学生而言,学习掌握现代理论工具需要花费巨大的时间和精力;另一方面,参透工程领域的基本问题,找到恰切的理论工具,更加具有挑战性。这种工作具有相当的难度,同时工业界并不珍视,在学术界也是偏离主流的冷僻方向,因此我们团队中有多名学生转向了更加实用热门的方向。但是我们相信,与追求发表论文和索引数目相比,解决基本问题更有长久的历史价值。
我们期待,在不远的将来,最优传输的几何算法、基于复线丛示性类的CAD算法会被工业界所采用;我们更期待,最优传输理论会成为AI教材的经典内容,复线丛示性类理论会成为CAD教材不可或缺的章节。我们对未来充满信心!
作者:【老顾谈几何】邀请国内国际著名纯粹数学家,应用数学家,理论物理学家和计算机科学家,讲授现代拓扑和几何的理论,算法和应用。
声明:首发老顾谈几何公众号(ID:conformalgeometry),部分图片源自网络,如有不当请联系我们,欢迎分享。




