探究薄板的纵向屈曲
一、背景:
在一些船舶,例如客船和客滚船的结构设计中,经常接触到比较“薄”的板。而目前规范对于板的屈曲校核普遍采用较为“统一”的方法,并未对“薄板”与“厚板”做区分。那对于“薄板”,我们现有的规范适用吗?笔者最近读到一本书《Trends in Analysis and Design of Marine Structures》,书中文章结合试验,研究了薄板的屈曲性能,很有意思。笔者结合自己对屈曲、薄板屈曲的理解和大家一起对这个问题做一次讨论。
二、问题:
近年来,随着规范越来越复杂,计算工况越来越多,屈曲校核过程有“流程化”、“无脑化”的趋势,用工程软件自动加载、校核而后看“红绿灯”是常规操作。借“薄板”这个话题来重新思考一下屈曲问题,相信会有所收获。同样的,课本知识 梁理论 有限元的组合拳是我们分析和研究的利器。
在展开讨论之前,有几个问题可以帮助大家思考:
1) 多厚是“厚”,多薄是“薄”?
2) 书本如何推导板格的纵向屈曲?
3) 规范是如何规定板的屈曲能力的?
这里,笔者抛砖引玉给出一些参考。
问题1):首先板的厚与薄是相对的,我们要引入合适的无量纲参数作为比较。从书本中可知一般情况下纵骨架式板格的(欧拉)纵向屈曲应力可表示为:
![]()
t为板厚,s为骨材间距。可见,t/s是一个直接平方关系影响屈曲强度的无量纲数。板的厚与薄应该从t/s来考虑。而船舶海洋工程结构物,s一般在500mm到800mm的范围,常规t从5mm到30mm的范围。规范中对屈曲问题,考虑到建造、初始缺陷、焊接应力、破环案例、材料等等因素,公式也复杂一些。规范的无量纲参数β考虑了材料的屈服应力和杨氏模量:

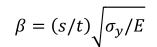
可见,s一定时,t越小,β越大。一般油船、散货船的β都在3以下,而客船、客滚船的β可达3~5甚至更大到6。我们可以以β = 3为线区分所谓的“薄”和“厚”。
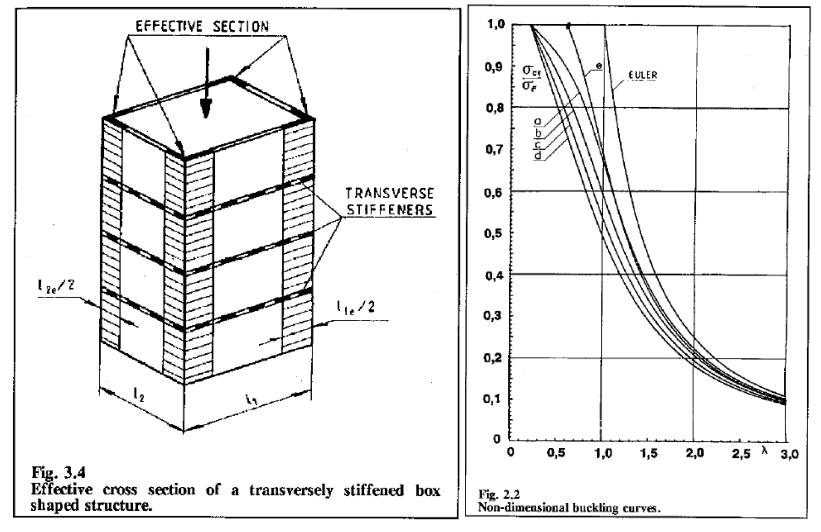
另外,需要注意规范定义的初始缺陷的上限亦以s为基准(而不是t,如下图所示),为s/200。这点比较容易被忽略,但它是屈曲分析的一大前提,后面将展开讨论。
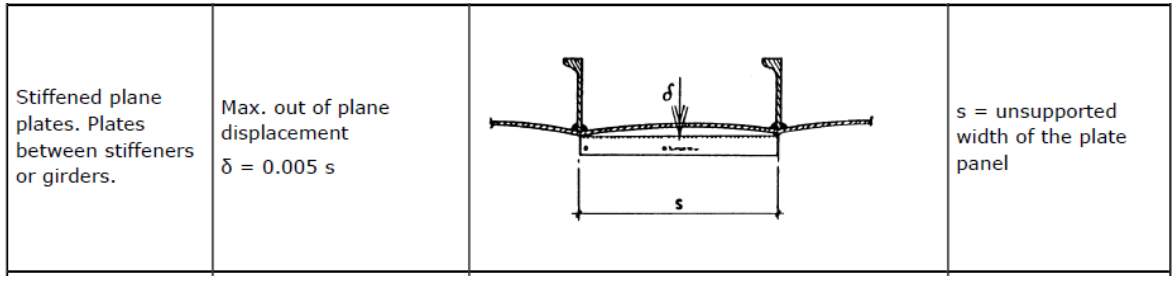
问题2)
翻阅书本可知,板的稳定性问题是分两步走的,临界(弹性)屈曲和后屈曲。
板的临界屈曲求解是从板的中性平衡微分方程(即板在面外载荷q作用下的弯曲问题)入手的。然后考虑板的中性面受压力和剪力,并令q=0,求解板的平衡解。这与求解压杆稳定性,从梁的复杂弯曲入手,套路是一样的。
公式推导这里不再列举,这里是笔者自己对书本内容的工程理解,仅供参考和讨论,也欢迎指正理解不到位的地方。
(1) 板在中面受压时,除了在受压方向上的中面“压缩”这个“解”之外,(数学上)在一定条件下还能“触发”面外方向上的“解”,即板“拱”或“凹凸”起来。
(2) 这个条件由压载荷的值达到一定大小后“触发”。压杆表达为欧拉力公式,板表达为欧拉应力公式,弹性范围内是仅和几何和材料弹性模量、泊松比有关的值。
(3) 与中面压缩这个解不同,面外方向上的“解”一旦触发,板格即失去稳定性。这个可以从两方面理解,首先在数学求解上得到的只是板面外变形的“形式”,对其具体“幅值”,求解过程并无直接“限制”(可以通过引入能量法来做一定约束);从刚度上理解,板一旦出现较大的面外变形,其面内的“轴向刚度”会失去作用,而换由板的“弯曲刚度”来抵抗面内载荷,而弯曲刚度是比轴向刚度要小得多。
(4) 书本上这部分内容是从数学推导出发的,理论上适用性很广,并无“厚”和“薄”的区别。
板的后屈曲性能是区别板和压杆屈曲的重要特点,即临界屈曲后的“应力重分布”。当板格的β较大时(即所谓薄板),板格容易发生弹性屈曲,若板的边界能提供有效支撑则板格能够继续承载,此时载荷主要由靠近边界的“有效宽度”来承担直至屈服,如下图所示。
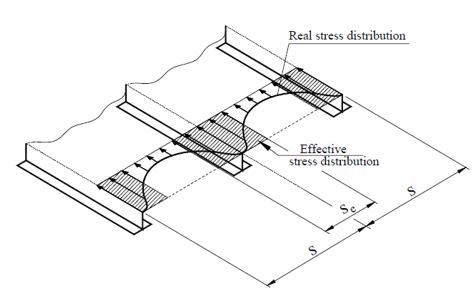
书本上将一般情况下的有效宽度假设为两边各0.22s。笔者认为其不一定适用于薄板的情况。根据截面Type III(参考DNV-OS-C101, Appendix A)的要求,取板厚的某个倍数,如15倍左右的板厚比较适合。
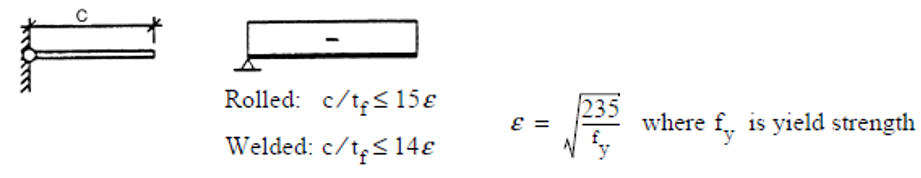
问题3)
书本和规范中对于不考虑应力重分布的板,其临界应力σcr的计算分两步,先计算欧拉应力σE,它仅和几何及弹性模量E、泊松比ν有关。若σE /σy<=0.5,则σcr =σE,若σE /σy >0.5,则做修正得到σcr。即:
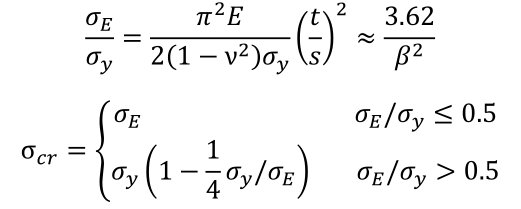
书本中,对于考虑应力重分布的板格的极限强度σu,表示为:
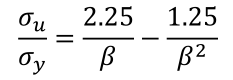
船舶共同规范CSR的定义为:
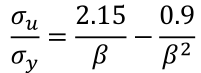
海工规范以DNV-RP-C201为例,形式上也基本相同(ϒM为大于1的材料系数,一般为1.15):
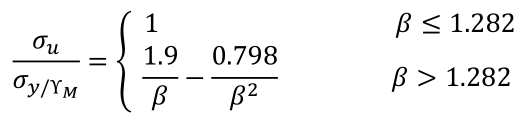
三、试验(数据引用于参考的文章)
参考的文章中,对一组矩形盒子经行了静压溃试验。试验尺寸和结果,以及CSR规范、有限元的评估结果如下,σy = 350MPa。
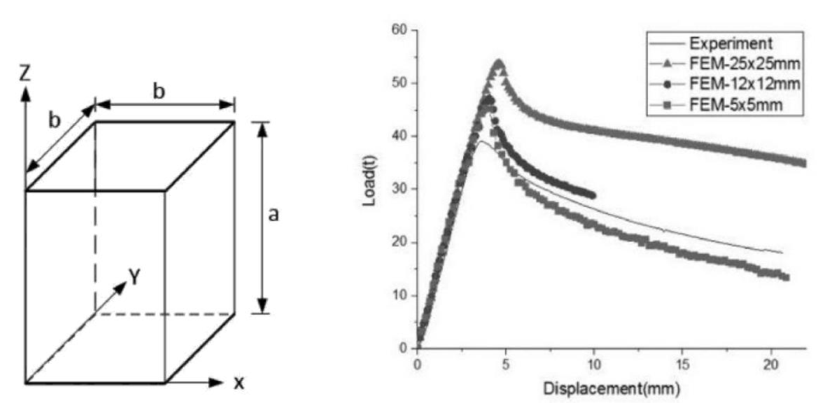
Model ID | Dimensions a x b x t (mm) | b/t | β | 试验
| CSR规范 | Nonlinear FEA in paper |
M-250 | 500 x 250 x 2.9 | 86.2 | 3.55 | 0.40 | 25% | 13% |
M-320 | 640 x 320 x 2.9 | 110.3 | 4.54 | 0.33 | 31% | 10% |
M-390 | 780 x 390 x 2.9 | 134.5 | 5.54 | 0.29 | 34% | 7% |
由于CSR规范和有限元的结果都大于试验值的结果,参考文章提出了当前船舶CSR规范和有限元结果都会高估所谓薄板屈曲性能的结论,并对规范做了进一步修正。
四、讨论
从公式出发
终于到了自由讨论环节。笔者有意在展示试验数据前,先介绍了诸多书本上的内容作为铺垫,作为接下来自己分析的参考。直观上,对文章的结论有些补充想法。
首先,CSR共同规范作为油船、散货船规范,虽然高估了试验结果,但值得注意的是这个误差似乎很稳定(至少比有限元的结果稳定)。再有,在非线性有限元计算中,关于初始缺陷的问题没有具体的介绍,试验前应仔细量取“初始缺陷”,并在有限元分析中充分考虑。
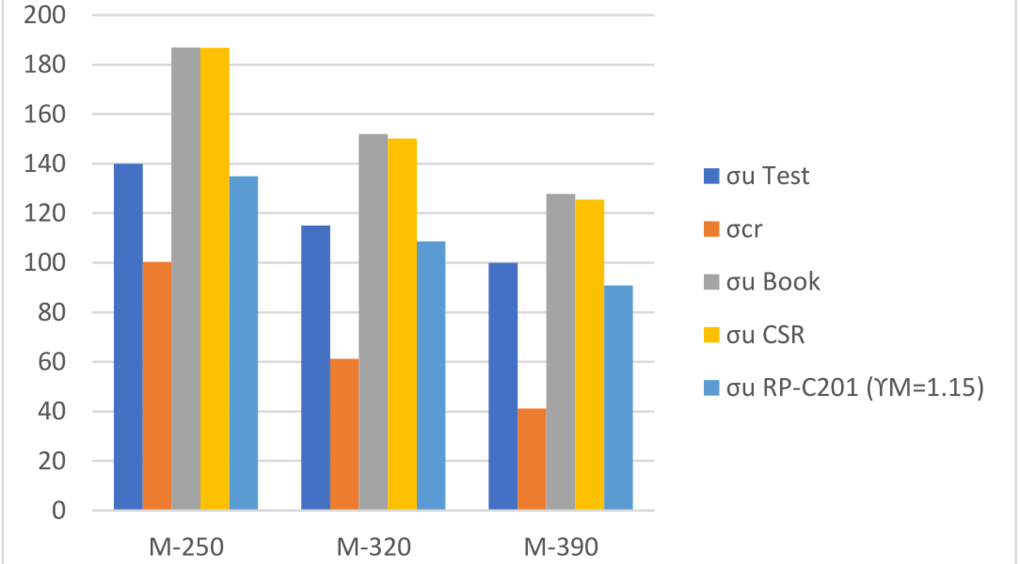
我们先来考虑σcr、书本上σu以及海工规范RP-C201的计算结果及其相互比较如下:
Model ID | b | t | σy | β | σu Test | σcr | σu Book | σu CSR | σu RP-C201 (ϒM=1.15) |
M-250 | 250 | 2.9 | 350 | 3.55 | 140 | 100 | 187 | 187 | 135 |
M-320 | 320 | 2.9 | 350 | 4.55 | 115 | 61 | 152 | 150 | 109 |
M-390 | 390 | 2.9 | 350 | 5.54 | 100 | 41 | 128 | 125 | 91 |
从下面比较的结果看,书本和CSR规范虽然都“高估”了,但公式中没有包含安全系数,并且所谓“误差”的百分比相对比较“稳定”。从带安全系数的RP-C201(1.15的材料系数)的结果来看结果是可以接受的。另外,可以明确的是应力重分布对薄板屈曲性能的贡献很大,因为σcr明显低于最终得到的屈曲强度。
Model ID | σu Test | σcr | σu Book | σu CSR | σu RP-C201 (ϒM=1.15) |
M-250 | 1 | -28% | 34% | 33% | -4% |
M-320 | 1 | -47% | 32% | 31% | -5% |
M-390 | 1 | -59% | 28% | 25% | -9% |
从有限元出发
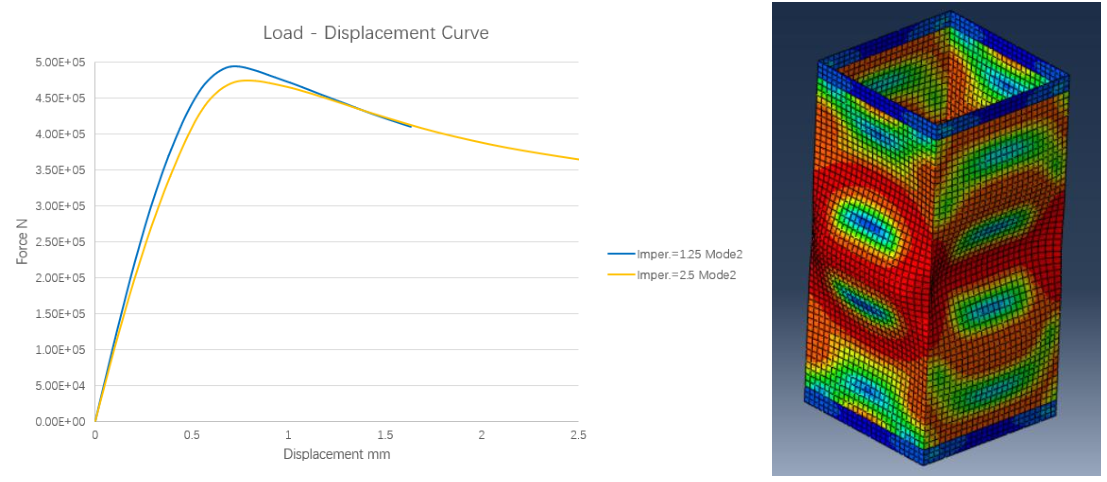
笔者对M-250模型,基于DNV-RP-C208,采用弧长法做了有限元压溃分析,并研究初始缺陷的影响。由于模型的长宽比为2,所以第一阶段模态(即两个半波,临界应力120MPa)为主要初始缺陷模态(Model1)。同时,还关注一个半波的模态(Model2,临界应力130MPa),因为它是焊接变形的常见形态。初始缺陷的幅值取s/200=1.25mm和s/100=2.5mm两个来分析其敏感性。
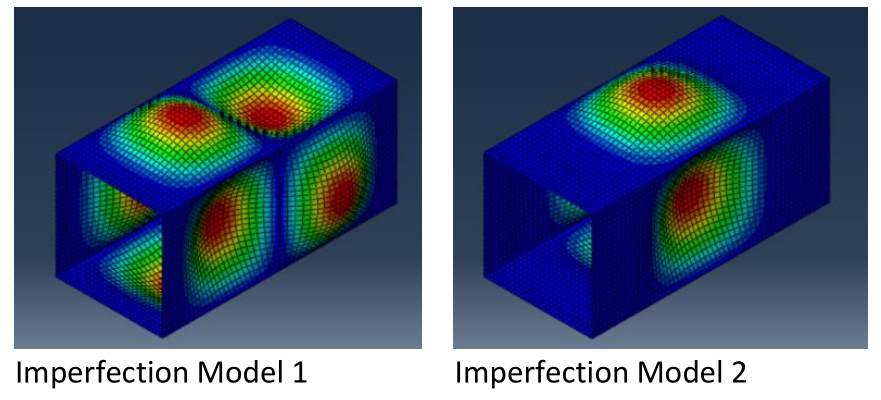
Model 1的结果
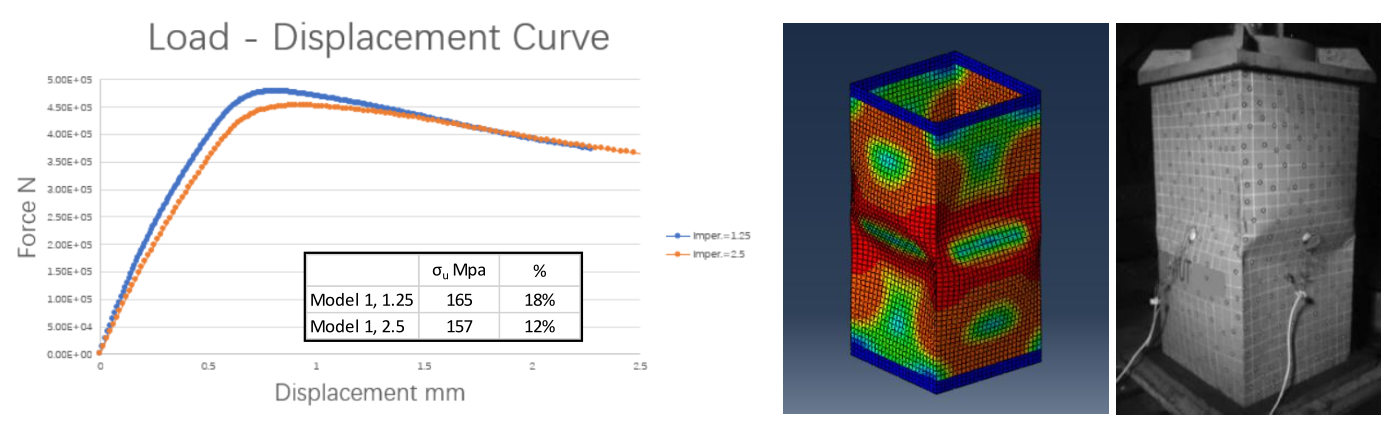
Model 1得到的结果,从结构极限状态的形式来看十分接近试验观察的现象。采用1.25mm和2.5mm的初始缺陷幅值,结果比试验分别大18%和12%。注意到若采用规范的安全格式,得到的结果应除以ϒM=1.15,则误差仅为2%和-3%。
Model 2的结果
Model 2得到的结果,从数值上接近(略高于)Model1的结果,但从结构极限状态的形式来看与试验观察的现象有所不同。
Model 3的结果
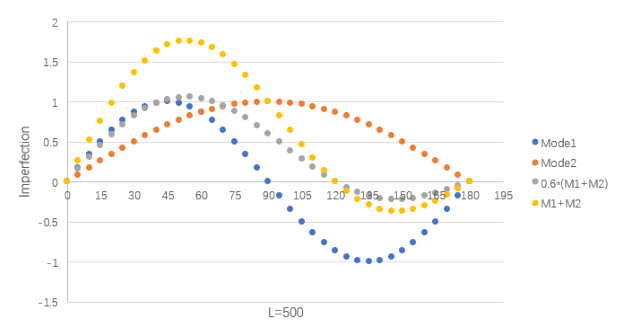
为了进一步分析初始缺陷的敏感性,可以引入Model3作为Model1和Model2的组合。沿着长边,板格的初始缺陷可直观地表达为下图。计算结果表面Model3的结果是接近Model1的,由此可知Model2的初始缺陷对结果影响不大(不敏感)。
五、综合讨论(梁理论登场)
经过了书本、规范和有限元讨论,我们对薄板屈曲的疑问是否得到解答?
笔者觉得通过有限元分析,可以明确对于β较大的板格,板的后屈曲强度(应力重分布)是问题的关键。
在本例中,应力重分布的结果是将截面“均匀承载”状态转变为板格的支持边界,即四个L梁主要承载的状态。30年前的规范中,有下图来说明这个问题。事实上,板格能否实现或者多大程度上实现应力重分布,主要取决于板格的支撑条件。在本例中,板格的边界实际上就是由如图所示的L梁来支持的。当L梁承担越来越多从板格上“转移”过来的载荷而达到极限/屈曲状态时,整个截面即达到极限承载能力。L梁的尺寸可以简单地根据上文中提到的Type III截面来考虑,本里中可取L33x33x2.9。L梁可取Cuvre C来计算其Column Buckling的强度。
本例中,L梁的屈曲强度约为85%x350=297.5MPa,设L梁之间的板格的屈曲强度为σcr =100MPa。则总的屈曲强度为153MPa。考虑ϒM=1.15的安全系数153/1.15=133MPa,这与RP-C201的结果几乎相同。可见用梁理论也可以验证屈曲强度的结果。
六、小结
综上所述,对于薄板的屈曲问题,因为临界应力较低,其问题的重点已经不在于板,而是支持板的筋和桁材。对于纵骨架式,纵向的力主要由筋来承担,横向的力主要由桁材来承担。而板(薄板)的主要“任务”是承担面内剪切载荷。筋和桁材是不承担面内剪切载荷的,它们只是作为板的“屈曲边界”而起作用。由书本可知,板的剪切临界屈曲强度要比单向屈曲强度要高出许多。
延申问题
这里给大家提几个延申问题,有兴趣的朋友可以思考一下。
1)在有限元Model1中提到有限元屈曲模态分析得到的临界应力为120MPa。而之前的理论结算得到的是100MPa。这是为什么呢?有限元得到的结果有没有问题?
2)规范定义的初始缺陷(变形)的量级为s/200,而一般常规s/t大约在50~60,意味着初始缺陷相比板厚要小许多。而薄板的s/t往往在80甚至100以上,即初始缺陷可以达到板厚的一半。如果初始缺陷的假设合理,对薄板来说是否意味着焊接的残余应力也格外重要?
关于更多船舶与海洋工程结构问题,欢迎关注笔者发布的课程《海洋平台强度分析》。





