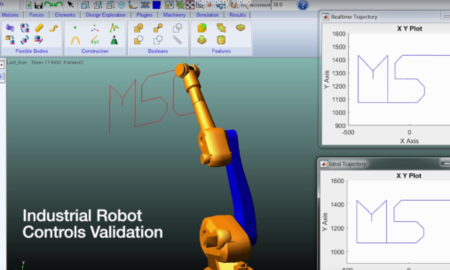
技术技巧 | 基于Adams实现滞回曲线
01
背景说明
Adams作为系统级的动力学仿真软件,对于零部件/总成的处理,通常是将其试验测得的外特性曲线引入软件中,以此代表零部件/总成的特性,比如用力-位移曲线表示螺旋弹簧、用力-速度曲线表示双 筒减振器、用轮胎模型(公式)表示轮胎特性等。
但是对于某些零部件/总成,其外特性存在滞回特性,即加载-卸载得到的特性曲线不重合,这种特性大多是因为系统阻尼造成的。
比如,对于钢板弹簧,由于其片间存在摩擦,使得刚度曲线存在滞回[2]。
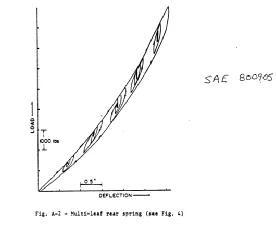
图1 多片簧刚度曲线
02 实现方法
零部件/总成不同,滞回曲线的机理及实现便会不同,本篇主要讨论三种情况。
对某些情况出现的滞回曲线,可以比较容易的判断是由于摩擦力产生的,且摩擦力易于用公式表示。
解决方法:在定义力的时候,定义摩擦力。
如粘滞摩擦:f=k*dz-c*vz。
在验证模型中,具体输入: func=10*(dy (marker_5, marker_6))-2*vz (marker_5, marker_6)
如库仑摩擦:f=k*dz-μ*abs(k*dz)*step(vr, -ε,-1,ε,1),其中step为换向函数,保证摩擦力的方向与运动方向相反。
在验证模型中具体输入:func=10*(dy (marker_5, marker_6))-0.2*abs (10*(dy (marker_5, marker_6))) *step (vr (marker_5, marker_6), -15, -1, 15, 1)

图2:验证模型

图3 力 粘滞阻尼

图4 力 库仑摩擦
上述方法可用于定义主销处摩擦力矩、管柱处摩擦力矩;也可以将两种阻尼结合使用来获得更加接近实际的滞回曲线。
用户可通过引入样条曲线(spline)的方式,定义刚度、摩擦系数等,进一步扩展函数的使用范围。
Bouc-Wen模型在工程上的应用非常广泛,有很多文献对其进行研究,主要将其用在模拟滞回曲线在汽车领域可将其应用到减振器曲线,钢板弹簧刚度曲线等。本节主要说明其公式在Adams中的实现,用到了状态变量、微分方程等建模元素。
根据参考文献[3],表达式为
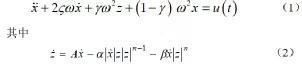
-DV_alpha*abs(varval(y_vel))*dif(z_dot) *(abs(dif(z_dot)))**(DV_n-1)
-DV_beta*varval(y_vel)*(abs(dif(z_dot)))**(DV_n)
x为正弦位移激励,通过上述微分方程,考察z(非线性滞回力)的变化趋势。
取文献中的两组参数进行计算,并与文献结果进行对比。
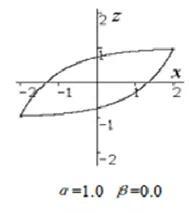
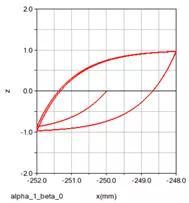
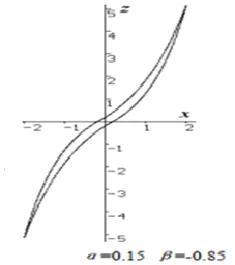
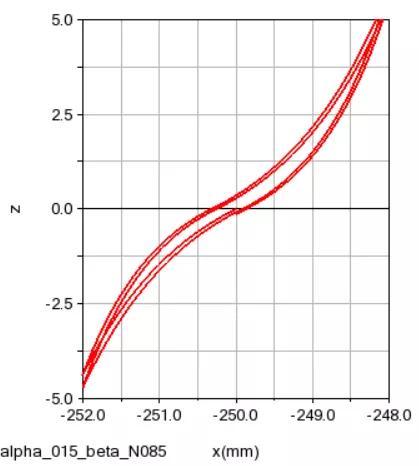
(左侧为论文截图,右侧为Adams计算结果)
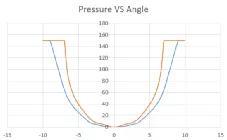
图6 液压转向机压力-角度曲线
此测试曲线来源于液压转向机的输入轴扭矩-压力测试结果,常规是将其等效为中间的平均线,与实际存在差异。
解决方案是,将其作为3D样条曲线(3d spline),自变量1为转角即横坐标,自变量2用来判断是加载还是卸载,对应蓝色及黄色曲线。
Step1:统一加载及卸载的横坐标,创建3d spline;
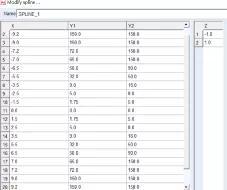
图7 创建后的3d spline表格
Step2:引用曲线
Akispl(.torque_3dspline.Az,step(.torque_3dspline.Az*.torque_3dspline.Wz,-0.001,-1,0.001,1),Spline_1)
Az表示第一自变量,即角度;
step(Az*Wz,-0.001,-1,0.001,1)为第二变量,即角度与角速度的乘积是负的(<-0.001),则此变量取-1,表示卸载;若乘积是正的(>0.001),则此变量取1,表示加载。
效果如下图。模型文件torque_3dspline.cmd。
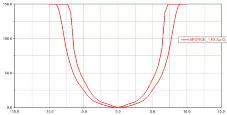
图8 Adams实现测试滞回曲线图
03 总结
本篇中,如2.1中主销处添加摩擦、2.3中的曲线引用,侧重于实现方法。体现Adams中step函数作为换向及方向判断的用途。
Bouc-Wen作为常用的表示迟滞的模型,Adams中已有使用(如Ride插件中的general bushing就用到了此方法),本文借助此模型,体现Adams中微分方程的用法,对于模型中的参数辨识及其应用未做细致研究。
04 附件
附测试模型,包括如下:
考虑摩擦力实现滞回曲线:spring_force_hysteresis.cmd
利用Bouc-Wen模型实现滞回曲线:spring_force_hysteresis.cmd(同上)
引用迟滞曲线:torque_3dspline.cmd
05 参考文献
[1] “Modeling Hysteresis in Adams”.
[2] “Measuremen and Representation of the Mechanical Properties of Truck Leaf Spring”, P.S. Fancher, SAE, 1980-0905.
[3] “Bouc-Wen滞回系统动力学特性的仿真研究”, 李宏光等, 系统仿真学报, 2004.09.040.