模态空间:为什么会产生谐波或谐阶次?
本文摘要(由AI生成):
本文主要讨论了谐波和旋转机械中的谐阶次问题。首先介绍了谐波的概念,即对周期性非正弦信号进行傅里叶变换所得到的大于基频整数倍的各次分量,通常称为高次谐波。接着介绍了与旋转机械相关的瀑布图或阶次域中,谐波被称之为谐阶次。然后讨论了谐波成分非傅里叶变换导致,以及如何通过声校准器校准麦克风的灵敏度。最后讨论了琴弦振动中的谐波,以及旋转机械中为什么会产生谐阶次。
导读:本文为谭祥军老师的原创作品,本文已授权,未经授权,严禁转载至其他各类平台,转发朋友圈或分享图文不受影响!
用户福利:为了帮助大家快速成长,为我国NVH行业扩充人才,NVH青年成长支持计划通过赠送三本NVH书籍(两本实体书,一本电子书)的方式支持部分NVH青年进行系统学习,期望大家在未来能为提高我国的NVH整体水平贡献力量。
一、写在前面
首先,我要说的是,对于这个问题的回答,我个人感觉不是那么完美,回答的过程中不乏脑洞大开,因而,欢迎拍砖指正。我的回答也算是抛砖引玉,希望大家集思广益,能提供更准确的答案。如果你对振动谐波产生的机理有所了解或有相关的资料,请不吝赐教。
这篇文章五一节前已准备好了,其实每篇技术文章都会尽可能的提前准备好,以便留出一些时间给自己细想:是否文中有不妥之处!
现实世界有许多旋转部件和系统的复杂机械经常会同时产生不同类型的振动和噪声问题。测量这些复杂机械的振动和噪声信号,我们可以将信号分解出不同的频率成分(阶次)。调查这些频域信息时,利用与机械设计的相关信息能指明哪些频率是由机械哪个部件产生的。这些复杂的机械结构如图1所示的内燃机发动机、涡轮发动机和液压泵等等。

(a)内燃机发动机

(b)涡轮发动机

(c)液压泵
图1 复杂机械的每个部件和系统都会产生特征频率(阶次)
二、谐波的定义
有时部件会因同一个现象(如振动的弦、房间的声模态或发动机的燃烧(如图2所示))产生多个相关的频率成分(阶次)。这些相关的频率成分称为激励的主要频率成分的“谐波”,而激励的主要频率成分称为“基频”。当试图去强调一个振动或噪声问题:通过修改一个会产生多个谐波的频率成分,一个基频可能会影响频域多个区域时,这个基频对于确定谐波的频率成分是非常有帮助的。
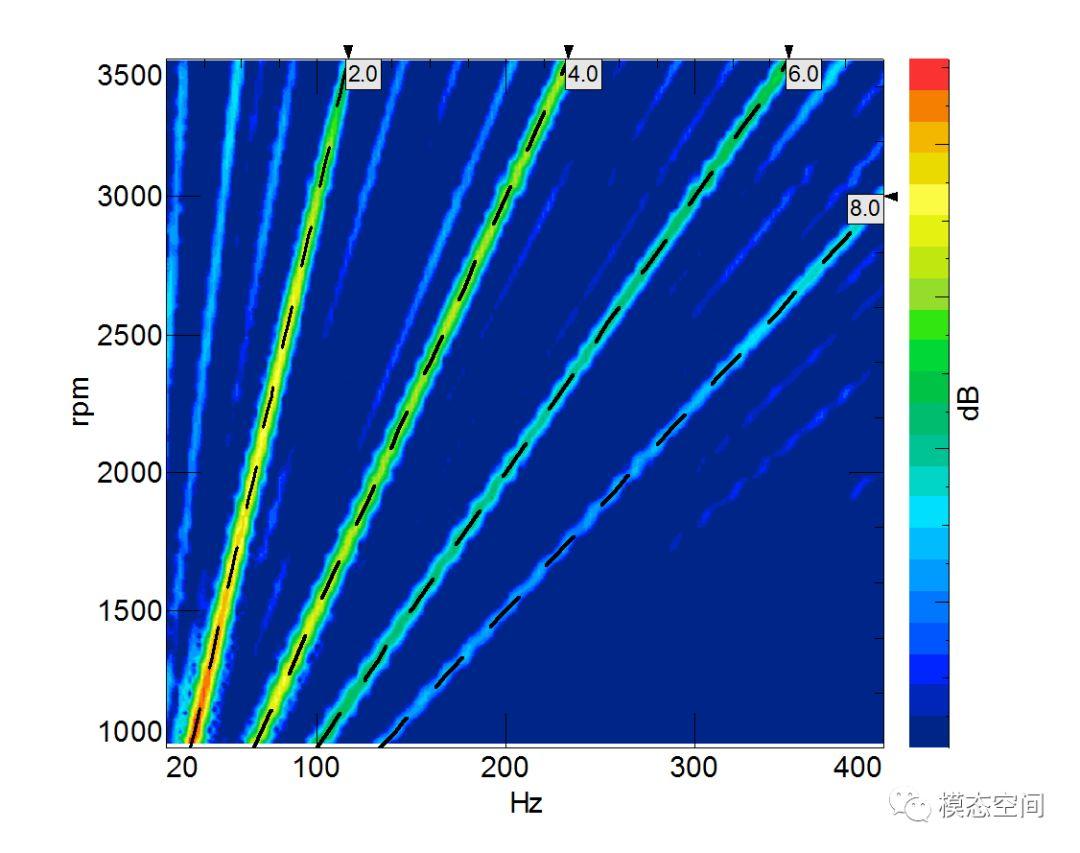
图2 4缸4冲程发动的点火阶次和前三个谐阶次
谐波是指对周期性非正弦信号进行傅里叶变换所得到的大于基频整数倍的各次分量,通常称为高次谐波。谐波的频率等于基频的整数倍,如基频3倍的波称之为三次谐波,基频5倍的波称之为五次谐波,以此类推。不管几次谐波,他们都是正弦波。基频整数倍的谐波也称为谐波分量。谐波分量在频域的频率成分称为谐频,如图3所示为工频50Hz的各个谐频成分。在与旋转机械相关的瀑布图或阶次域中,谐波被称之为谐阶次,如图2所示的4缸4冲程发动机的4,6,8阶次为点火阶次的谐阶次。

图3 工频及其谐频
三、谐波成分非傅里叶变换导致
我们经常使用声校准器校准麦克风的灵敏度,声校准器发出的声音频率为1000Hz,大小为94dB或114dB,我们以为这个声音是一个纯音。但实际上,不是!声校准器发出的声音的频谱如图4所示,使用对数幅值显示时,从频谱图上可以看出这个声音包含了1000Hz的多个谐波。只是二次谐波以上的分量幅值很小而已,采用对数尺度显示能方便地看出这些高次谐波分量。
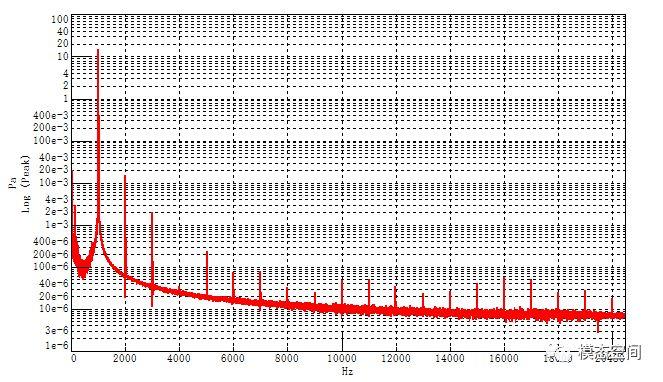
图4 声校准器发出的声音的频谱
由于信号从时域变换到频域需要使用傅里叶变换,那么,是不是图4的这些谐波分量是由傅里叶变换引起的呢?在这,由软件生成一个1000Hz的单频正弦波,然后,对这个信号进行傅里叶变换,得到的频谱如图5所示。从图5可以看出,即使使用对数幅值形式,频谱仍然只有1000Hz这个单一的频谱成分,没有其他谐波分量。这说明信号中的谐波分量不是由于傅里叶变换引起的,而是原始信号中就包含这些谐波分量。那什么为产生这些谐波分量呢?
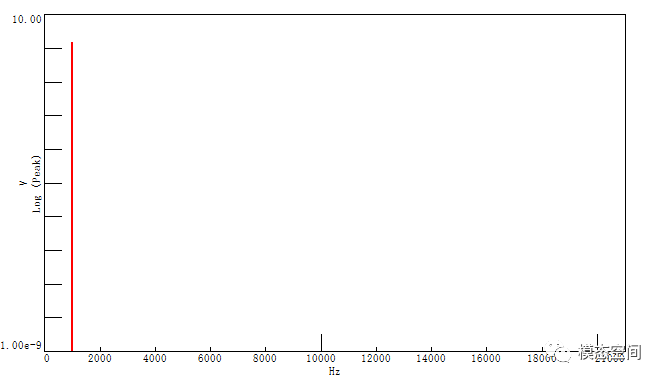
图5 软件生成的单频信号的频谱
四、包含谐波成分的常见信号的傅里叶变换
数学上最熟悉的谐波成分的例子之一是方波,如图6所示。它不像正弦波只包含一个频率成分,理论上而言,是由无穷的正弦波组合而成,这些正弦波的频率成分是基频的整数倍(高次谐波)。在方波中,只包含奇数倍的高次谐波,对于幅值为1,周期为2π/ω的方波信号,它的傅里叶变换为


图6 时域方波信号(左)和它的频率成分(右)
对于幅值为1,周期为2π/ω的三角波信号(图7),它的傅里叶变换为
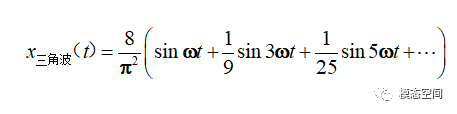

图7 周期三角波
对于幅值为1,周期为2π/ω的锯齿波信号(图8),它的傅里叶变换为
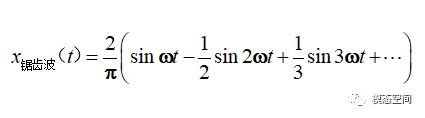

图8 周期锯齿波
对于幅值为1,周期为2π/ω的周期半波余弦信号(图9),它的傅里叶变换为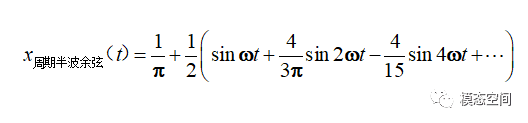
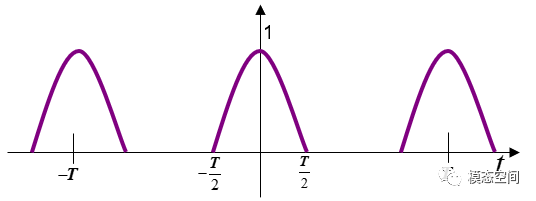
图9 周期半波余弦信号
对于幅值为1,周期为2π/ω的全波余弦信号(图10),它的傅里叶变换为
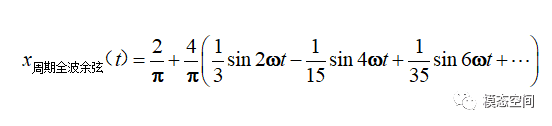
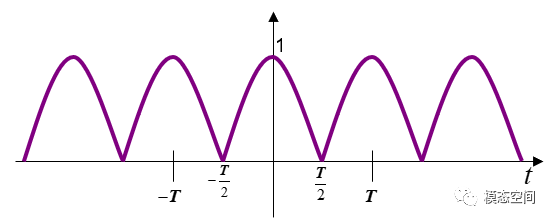
图10 周期全波余弦信号
由方波和三波信号的的傅里叶变换可知,它们的频率成分包含奇数倍的高次谐波;由锯齿波和周期半波余弦信号的傅里叶变换可知,它们的频率成分包含整数倍的高次谐波;由周期全波余弦信号的傅里叶变换可知,它的频率成分包含偶数倍的高次谐波。
如果激励信号是包含多个谐波成分的信号,如方波、三角波、锯齿波等,那么,必然在响应中也存在这些谐波成分。在电动汽车的交流电转换成直流电的过程中,就存在半波整流(图9)或全波整流(图10),对于单相半波整流而言,电路中的频率成分是1倍的线频率;单相全波整流电路中的频率成分为2倍的线频率。
对于三相整流而言,半波整流的频率为3倍的线频率;全波整流的频率为6倍的线频率。如果控制器出现问题导致某相交流电丢失,则信号频率将出现其他倍频(谐频)。如果在三相全波整流中出现高的2,3,4和5倍线频率,则表明整流电路出现了问题,这些倍频都是问题频率,在信号的频谱中会体现出来。
五、琴弦实例
相类似,如果我们拨动一根琴弦(如吉它的琴弦),将能激起多个谐波。每个谐波都会有不同的振动模式或模态振型。当我们拨动琴弦时,能听到同时被激起来的所有模态产生的声音。因为琴弦两端约束,所有的谐波模态频率都是第一阶模态频率的整数倍(高次谐波),第一阶是基频。图11给出了拨动的琴弦的基频至第6阶谐波的模态振型。
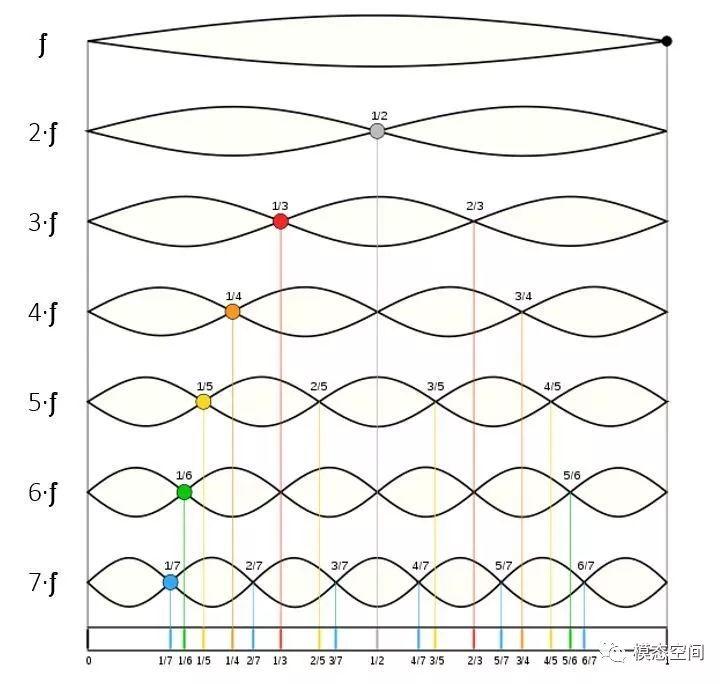
图11 振动琴弦的前7阶模态振型
取决于怎样和在什么位置拨动琴弦,可以激起所有的谐波,或者可能只是它们其中的少数几个。激励起来的谐波数量与大小将决定振动琴弦产生的声音。如果拨动琴弦的位置靠近中点,那么在中点没有节点的奇数阶谐波被激励起来的幅度远大于在中点有节点的偶数阶谐波。如果我们观察琴弦的平均频谱,我们能看到这些谐波以及它们的相对大小,如图12所示。

图12 琴弦平均频谱中的谐波成分
因此,当系统被激励起多个谐波分量时,必然会在频谱中体现出来,像信号是方波、三角波等,这些谐波的频率是基频的整数倍。
六、为什么会产生谐阶次
对于旋转机械而言,除了转频对应的1阶次之外,经常还会出现谐阶次的情况,如图2中的点火阶次的谐阶次,这又是什么原因造成的呢?如果激励信号中包含多个谐波成分,那么,同样地,也会在旋转机械的响应信号的频谱中有体现。但对于旋转机械而言,与前面所述的琴弦又有差异。
在回答这个问题之前,让我们简单回顾一下阶次的概念。在文章《怎么理解阶次?》一文中,我们已经清楚地说明阶次的物理意义是表示旋转一圈,事件(振动噪声等)发生的次数。
1阶次表示每旋转一圈,事件发生1次,2阶次表示每旋转一圈,事件发生2次,n阶次表示每旋转一圈,事件发生n次。如齿数为51个的齿轮,在振动噪声信号中的51阶次,我们都能很好的理解,因为51个齿在每旋转一周时,轮齿需要啮合51次,对应的阶次为51阶次。那102阶次,153阶次或者更高阶次,又是什么原因导致产生的呢?
对信号分析得到的阶次可以看成是转轴阶次与齿轮阶次的乘积。如果转轴是1阶次,而齿轮的制造、安装和几何都完美,51个齿对应51阶次,那么,二者的乘积将是51阶次(啮合阶次)。而对于102阶次或者更高阶次而言,就存在三种可能性:一种是谐阶次仅来自转轴;另一种情况是谐阶次仅来自齿轮;第三种情况是二者都有其他的高阶谐阶次。
首先讨论第一种情况:谐阶次仅来自转轴,假设齿轮制造、安装和几何都完美。对于旋转轴而言,如果仅存在不平衡、轴弯曲或偏心,那么只会引起1阶次的振动。但通常存在轴系不对中的情况,并且这种现象还非常普遍。不对中包括三大类型:
i)角度错位:轴中心线相交但不平行,如图13a所示;
ii)中心线偏置:轴中心线平行但不相交,如图13b所示;
iii)二者组合的结果。但现实当中不可能是单独一种不对中的类型,通常是两种类型的组合。
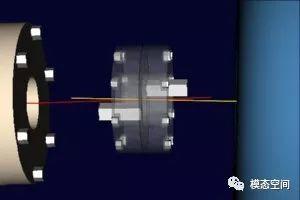
(a)角度错位
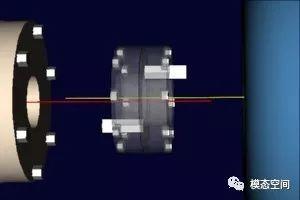
(b)中心线偏置
图13 两种轴系不对中类型
轴系不对中会导致出现2阶次,3阶次或更高阶次。通常角度错位不对中会使信号的频率成分除了有较高的1阶次之外,还有较低的更高阶次,如图14所示。
而中心线偏置也会出现高阶次,但通常2阶次分量更大,如图15所示。如果转轴出现了2阶次及以上的高阶次,那么,轴系的阶次乘以齿轮的阶次,必将导致测量的信号中会出现更高阶次,如之前51个齿的齿轮的102阶次、153阶次等。

图14 角度错位对应的频谱

图15 中心线偏置对应的频谱
中心线偏置类型的不对中会引起高的2阶次(2倍频),除此之外,转子热态不对中、裂纹、松动、水平方向上支承刚度过差等,也都会引起2阶次振动分量增大,绝大多数是轴系不对中。(其实感觉又进入了死循环:轴系的这些高阶次又是怎么产生的呢?想哭……)
在《电机定子模态的空间特性》一文中,讲到电机的径向电磁力波或定子的模态振型会出现如图16所示的形状。如果转轴是按这样的形状旋转,也就是轴心轨迹(利萨如图)是这样的形状,那么转轴必然出现相应的n次谐阶次,如n=2,则出现2阶次,n=5,则出现5阶次。
我们知道模态分析得到的各阶振型向量是模态空间的“基向量”,任何测点处的响应都是各阶“基向量”与相应的模态坐标(贡献量)的乘积的叠加,那么,在这里,我也可以认为图16所示的各个轴心轨迹是实际轴心轨迹的“基向量”,轴的实际轨迹是这些“基向量”与相应的贡献量(系数)的乘积的叠加,由于贡献量的大小不同,导致各阶次的幅值高低不一样(见图14和15),因而,将会导致在轴系的频率成分中出现基频及其高次谐频。
这时,必使齿轮(或其他旋转结构,如风机、泵等)的振动噪声信号出现高阶谐阶次。在诸自强教授的《电机噪声的分析与控制》一书中第247页中讲到,加于轴承的轴向负荷引起了交变挠曲弹性变形振动,可以这样来看,由于轴向负荷使得轴承所有的钢球对轴承外圈施加等距离的径向负荷,从而使得轴承外圈从圆变成多少有点多边形。
这也验证了轴承的变形使转轴会出现高阶谐次。(这段话属于脑洞大开,欢迎拍砖!如果哪位仁兄可以按这个思路去模拟验证一下,那就最好不过了。)
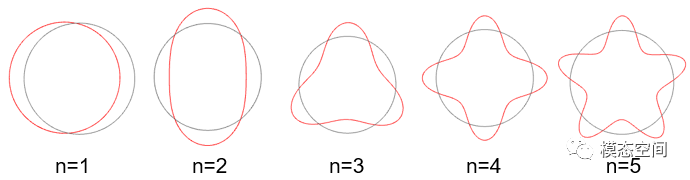
图16 电机的径向电磁力波形状或定子模态振型
现在讨论第二种情况:谐阶次仅来自齿轮,假设轴系安装、刚度都完美,使得其旋转过程中只有1阶次。齿轮自身的高次谐波需要从两个方面着手,一个方面与齿轮的几形变形相关;另一方面与齿的啮合相关。也可以按静态误差和动态误差来分类。
静态误差主要是指齿轮制造误差和几何误差,而动态误差是指啮合过程中受到周期变化的作用,如啮合刚度的变化,载荷的变化,温度的变化等。
对于完美啮合的齿轮而言,不存在几何变形,偏心或对中等问题,则只有啮合阶次,如之前例子中的51阶次。但是由于制造误差等原因将导致齿轮偏心或几何变形,如变成了椭圆,如图17所示,虚线表示完美的齿轮,这时将会出现2阶次,因为椭圆有一根长轴,旋转一圈时会发生两次碰撞,因此,对于51个齿的齿轮而言,几何形状变成椭圆则会出现102阶次。
齿轮几何形状的变化将导致齿轮啮合时存在径向跳动,径向跳动周期相对于啮合周期而言,周期更长,因此,是一种低频的运动,如图18所示。这是一个齿数为51个的齿轮的径向跳动波形,从图中可以看出,径向跳动的周期刚好是旋转一圈对应的时间长度。
如果是椭圆形状,则径向跳动对应2阶次,其频率成分远小于啮合阶次51阶次。当然如果齿轮变形如图16所示,那么,必然出现高阶谐阶次。(这个似乎会引起调制。)
对于齿轮的变形我们也可以遵循之前转轴的轴心轨迹的思路。把图16认为变形的基向量,实际变形是这些基向量的叠加,那么,同样地道理,齿轮也会出现各个谐阶次。(这段话仍属于脑洞大开,欢迎拍砖!)

图17 制造误差引起齿轮啮合不完美
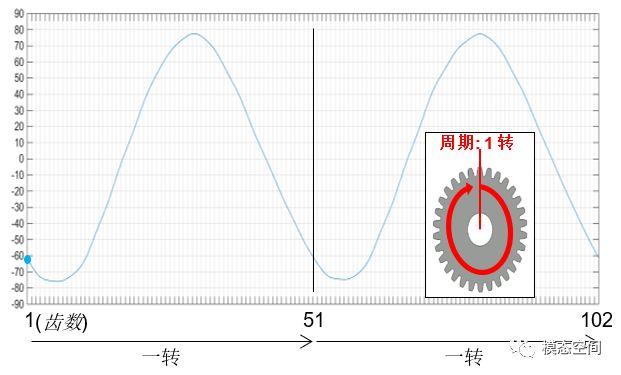
图18 径向跳动是一种低频激励
另一方面的原因与齿的啮合相关。在齿轮的啮合过程中,由于主动轮与从动轮的单、双齿啮合交替变换,啮合位置、轮齿啮合刚度和载荷的周期性变化(请参考《浅析齿轮结构NVH问题的产生机理》一文)会引起高阶谐阶次。另一方面,载荷的不平稳也会引起齿轮本身的刚度变化。
齿轮在装配过程中,可能会存在如下的装配误差:对中误差、角度误差、装配公差和结构变形等,这些装配误差也会导致类似轴系的高次谐波,从而使齿轮出现除了啮合阶次之外的高阶谐阶次。
另一方面,因轮齿和齿轮刚度的变化、轮齿微观几何误差、制造误差和装配误差等方面导致的齿轮传递误差也会产生高次谐波。这是因为传递误差是以1个啮合周期为周期,而齿轮的啮合频率高,因而这些误差导致的传递误差是一种低幅值高频的传递误差,如图19所示。
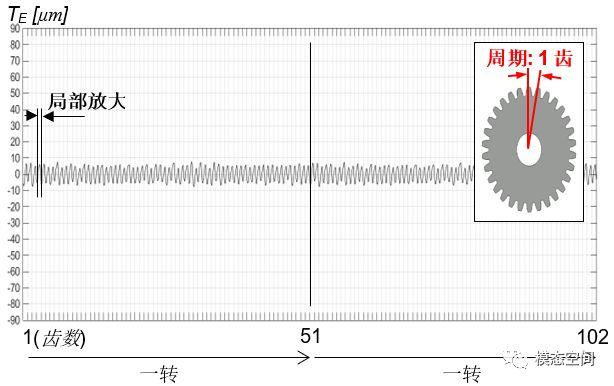
图19 齿通过激励造成的传递误差
局部放大一个齿周期内的传递误差信号,如图20所示,可以看出,传递误差幅值量级特别小,因此,要分辨出这些传递误差,要求极高的分辨率,从放大的一个周期的信号可以看出,这个信号不是一个正弦波,因此,不是一个单频信号,而是一个复合波形,这样就可能含有诸多的谐频成分。另一方面,由于是啮合过程产生的传递,因而,这些信号包含了明显的阶次成分。
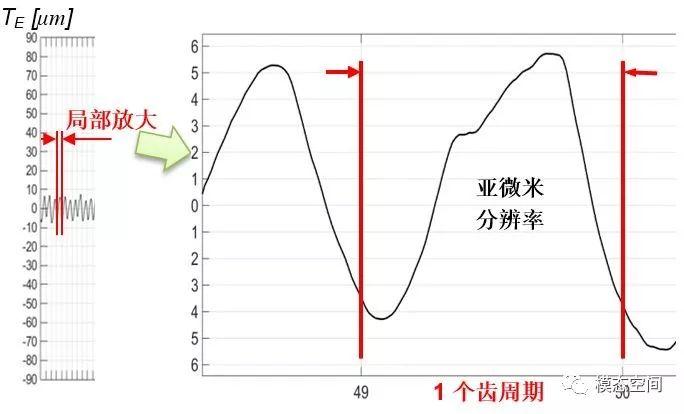
图20 齿通过激励造成的传递误差局部放大
以上说明的情况是高阶谐阶次分别仅来自转轴和齿轮的情况,但现实中更多可能情况是二者共同组合的结果,使得信号的频谱出现了高阶谐阶次。
在这里仅是以齿轮为例进行了说明,但实际上还有很多其他的旋转机械,如发动机、泵、风机等。虽然这些结构与齿轮有很大的不同,但二者也有相同之处,即都是通过转轴带动的,因此,对于轴系的谐次可以相同理解。
七、小结
谐波的产生不是由傅里叶变换引起的,而是原始信号中就包含这些谐波成分;
如果激励信号是包含多个谐波成分的信号,如方波、三角波、锯齿波等,那么,必然在响应中也存在这些谐波成分;
轴系的安装不对中、裂纹、松动等原因会导致产生2阶次及其以上的谐波;
齿轮因几何变形、啮合刚度变化、载荷周期变化等也会导致高阶谐阶次;
齿轮的高阶谐阶次可能来自于轴系,也可能是齿轮本身,或者是二者共同作用的结果;
其他旋转机械的高次谐波可同等理解。
参考资料
[1] http://www.vibrationschool.com/mans/SpecInter/SpecInter06.htm
作者:谭祥军 模态空间主编 仿真秀特邀专栏作者
声明:原创文章,首发模态空间公 众号(ID:modalspace),本文已授权,部分图片源自网络,如有不当请联系我们,欢迎分享,禁止私自转载,转载请联系作者。







