基于Abaqus金属管压力成形过程和成形极限图
本文摘要:(由ai生成)
本文讨论了使用Abaqus模拟金属管液压成形的过程,重点在于避免成形过程中的失效模式,如颈缩和破裂。通过成形极限图(FLD)评估材料的成形性,预测断裂失效。模拟展示了应力/应变结果、FLD损坏标准结果和壁厚结果,帮助优化模具几何形状和工艺设置。讨论强调了液压成形工艺的优势,以及有限元分析在预测应力/应变、评估材料成形性和优化工艺参数中的重要性。
目录
介绍
优点
失效模式
失效准则 - 成形极限图 (FLD)
有限元模型
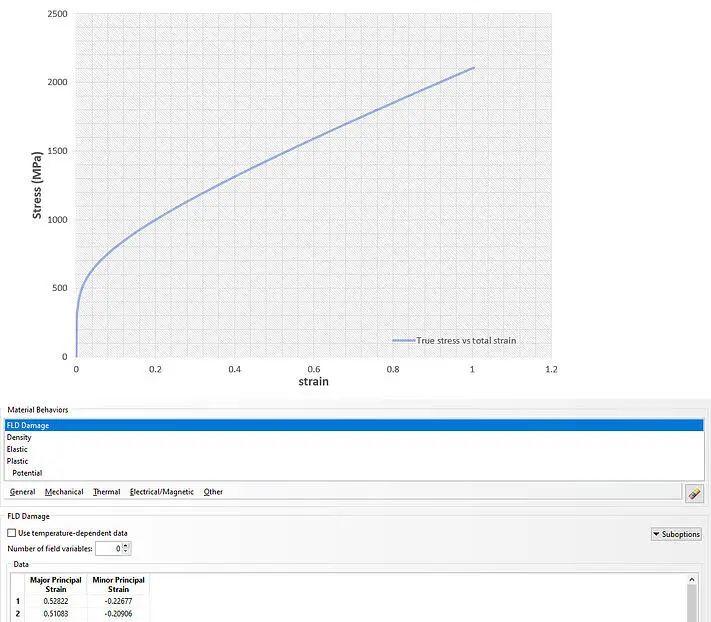
材料特性
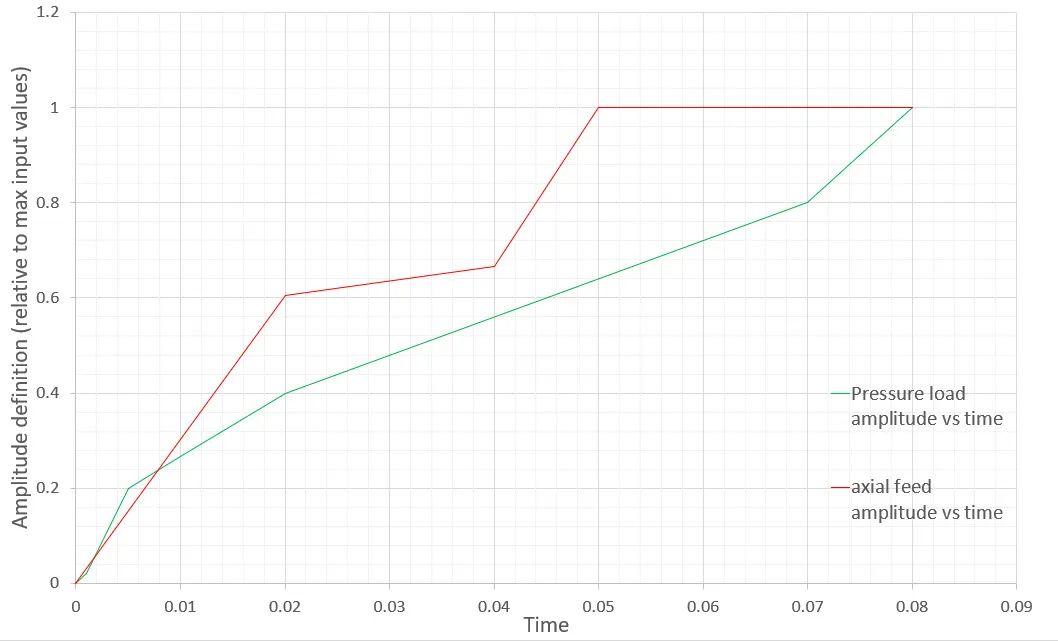
加载
结果
应力/应变结果
形成极限损坏标准结果
壁厚结果
讨论
在这文章中,我们将讨论使用 Abaqus 进行金属管液压成形的模拟。采用成形极限图来创建材料的应变包络线,以避免颈缩(破裂),这是此类金属成形过程中可能的失效模式。这将在金属波纹管接头的液压成形过程模拟中得到证明。
介绍
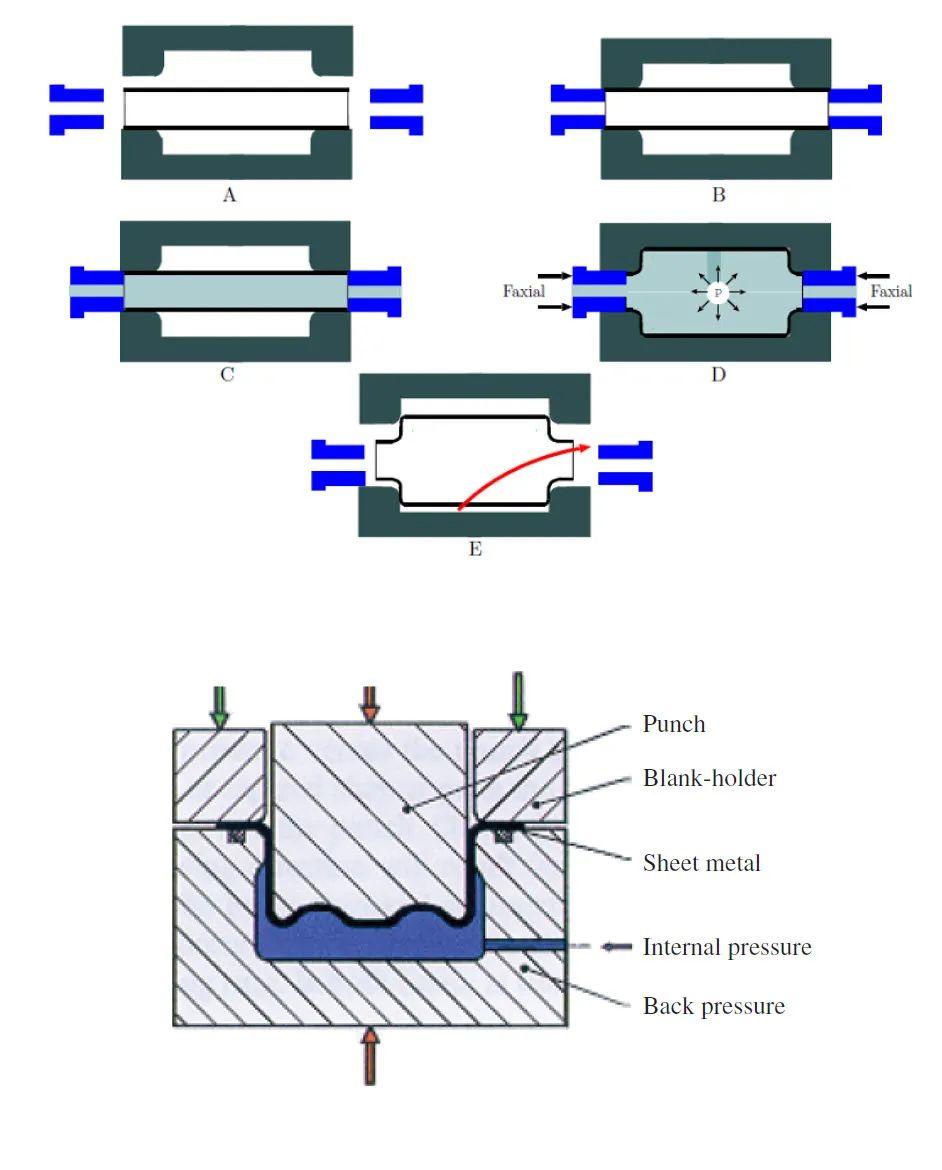
优点
减轻重量, 壁厚均匀, 降低工具成本(更少的部件=更少的停机时间,更简单的工具设计), 增加刚度, 减少二次操作的数量, 提高尺寸精度, 减少废品。
失效模式

失效准则 - 成形极限图 (FLD)
成形极限图 (FLD) 通常用于金属钣金成形工艺中,以评估工件的成形性并避免潜在的故障。这些是根据双轴应变状态下的主应变与次主应变图形成的。作为一项较新的进步,使用了成形极限应力图 (FLSD),因为它们对应变路径变化不敏感。
FLD 是通过特定测试通过实验获得的,是液压成形过程中断裂失效的可靠预测指标。为了考虑与实验数据输入相关的不确定性,通常会引入特定材料的成形极限曲线 (FLC) 的安全裕度。
示例中使用的高强度双相钢的 FLC 曲线如下图 3 所示,以浅蓝色显示(“exp”)。这是通过测试得出的。还显示了示例性设计安全曲线(“安全性”),以及特定钢的某些材料状态的限制线。发生某些故障模式的特定区域也在图 3 中以粗体注释。
 图 3:高强度钢的 FLD
图 3:高强度钢的 FLD
有限元模型
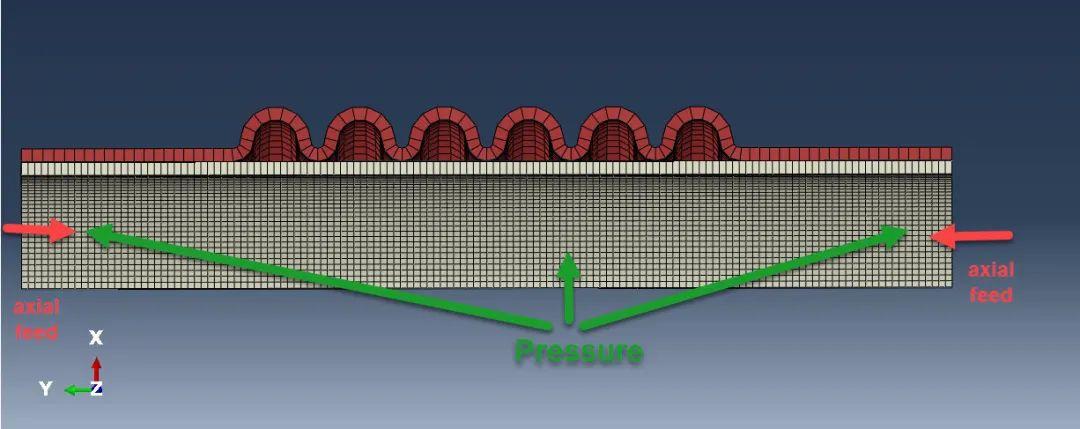
材料特性
加载
结果


形成极限损坏标准结果
跟踪 FLD 损伤 (FLDCRT) 将有助于深入了解材料的成形性限制。这可以帮助评估不同的材料并针对特定的液压成形工艺或模具形状决定最合适的材料。
FLD标准的结果如下所示。只要 FLDCRT 保持在 1 以下,材料点就会保持在图 3 的极限曲线下方。对于波纹管示例,材料保持在成形极限内,直到过程完成前 0.01 秒。
在液压成形模拟结束时,在样本 (FLDCRT>1) 最大塑性应变位置观察到失效。最后两帧的详细信息如下图 7 所示。
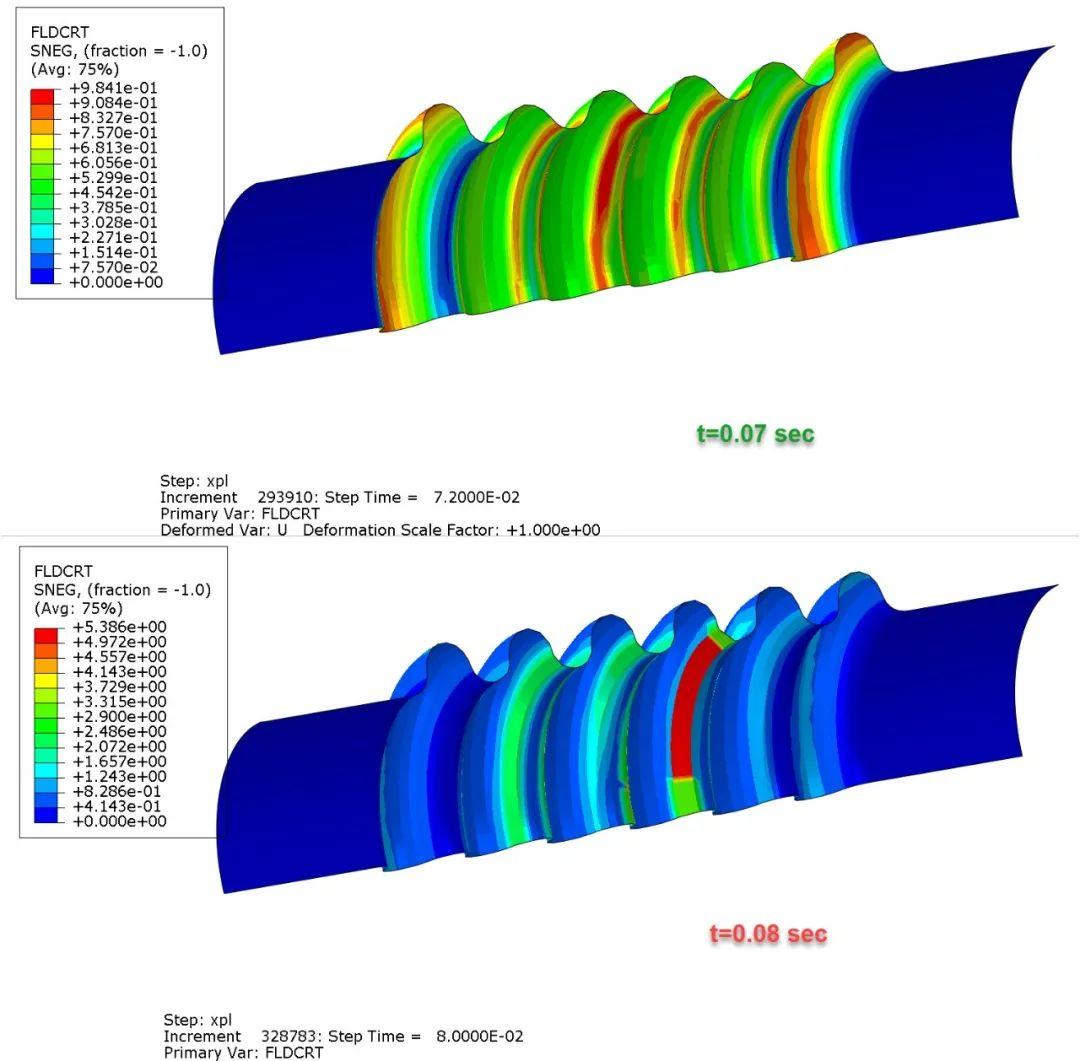
下面的视频给出了金属波纹管液压成形的 FLD 标准结果。

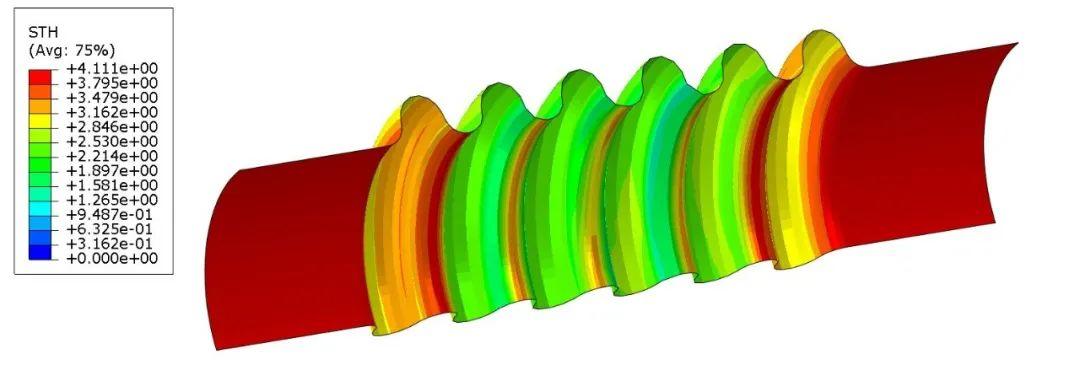
壁厚结果

讨论
在上一节中,介绍了波纹管液压成形模拟的结果。液压成形工艺由于其相对于传统成形工艺的上述优点而变得相当流行。
能够准确预测在此过程中产生的实际应力/应变, 可以实施 FLD 损伤来评估材料的可成形性,甚至保持在一定的 FLD 限制百分比以下, 可以研究模具工件摩擦特性并修改这些特性以获得波纹管的特定凸出高度, 通过优化例程最小化 FLD 百分比的可能性(可以使用 Isight 或类似软件), 评估特定液压成形工艺和/或工件几何形状的不同材料的可能性, 可以优化样本几何形状以消除应力热点, 可以优化液压成形工艺的加载路径参数,以实现最大的壁厚均匀性或保持在一定的厚度减少范围内(可以使用 Isight 或类似软件)。
登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2024-11-02
最近编辑:27天前
相关推荐
最新文章
热门文章





